Gegeben ist eine Funktionsschar fa(x) = x^4-ax^2
a)Zeigen sie rechnerisch, dass die Graphen der Funktionsschar für a<=0 keinen Hochpunkt haben.
f'(x) = 4·x^3 - 2·a·x = 2·x·(2·x^2 - a) = 0
für a = 0 gibt es nur einen Tiefpunkt an der Stelle 0. Für a < 0 hat die klammer eine doppelte Nullstelle und damit keinen Einfluss. Für a < 0 hat die Klammer keine Nullstelle.
b) bestimmen sie für a>0 die Ortskurve der Tiefpunkte und Wendepunkte der Schar.
2·x^2 - a = 0 → a = 2·x^2
y = x^4 - 2·x^2·x^2 = - x^4
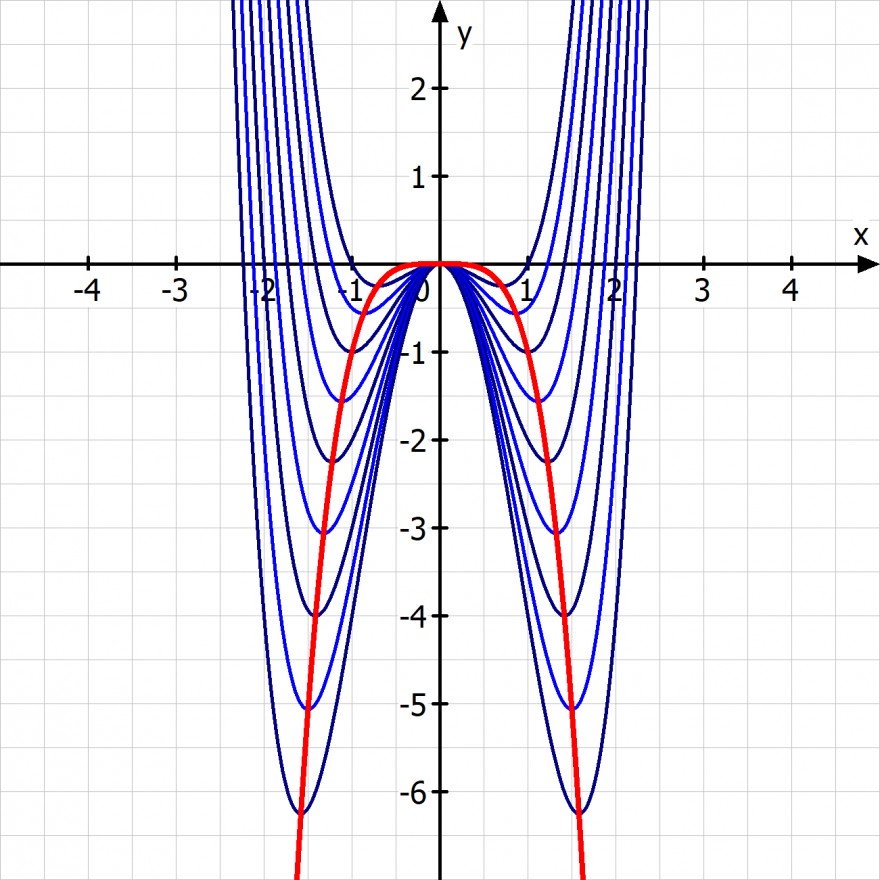
C) bestimmen sie die Gleichung der Tangente an den Graphen im Punkt P(1/f(1)). Für welchen Wert von a beträgt die Steigung -0,5?
t(x) = f'(1)·(x - 1) + f(1) = (4 - 2·a)·x + (a - 3)
4 - 2·a = -0.5 --> a = 2.25