Parameterfunktion f t (x) = 2x^{4}-4tx^{2}+2t^{2} . Ortskurven der Hoch- und Tiefpunkte davon?

Question

könnte mir einer die Ortskurven der Hoch- und Tiefpunkge zu 

f t (x) = 2x^{4}-4tx^{2}+2t^{2} 

nennen ?

Comments

Ortskurven von was?

---

Ortskurve der Hoch und Tiefpunkte

EDIT(Lu): "Hoch und Tiefpunkte" in der Fragestellung ergänzt. 

Answer 1

Hallo Exodius,

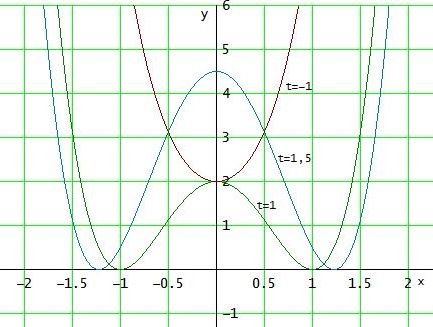
f_t (x) = 2x⁴ - 4tx² + 2t² 

f_t'(x)  =  8·x³ - 8·t·x  =  0     ⇔  8x · (x² - t) = 0  ⇔  x=0  oder  x = ±√t

Einsetzen ergibt die Extrempunkte ( 0 | 2t² )  und  ( ±√t | 0 )

Eine geschlossene Ortskurve gibt es nicht:

Die Extrempunkte liegen alle auf der x-Achse oder auf der positiven y-Achse.

Gruß Wolfgang

Answer 2

f(x) = 2·x^4 - 4·t·x^2 + 2·t^2

f'(x) = 8·x^3 - 8·t·x = 0 --> t = x^2 oder x = 0

Ortskurve: 

y = 2·x^4 - 4·(x^2)·x^2 + 2·(x^2)^2 = 0

Da die Funktion achsensymmetrisch ist sollten auch Extrempunkte auf der y-Achse liegen.

x = 0

Comments

Das ist deutlich zu knapp.

---

Ich war noch nicht ganz fertig.