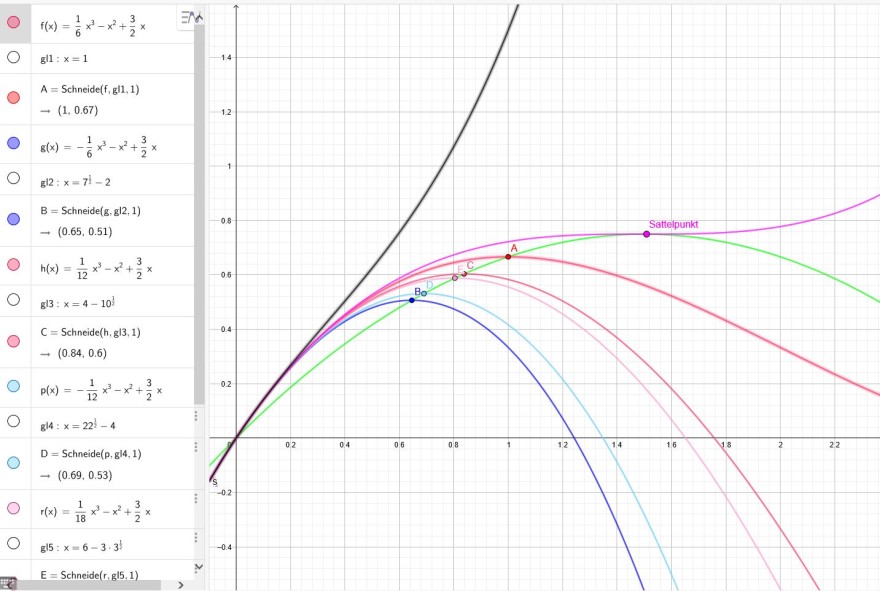
Gesucht ist eine Gleichung der Kurve, auf der alle Hochpunkte der Kurvenschar \( f_{k}(x)=\frac{1}{6 k} \cdot x^{3}-x^{2}+\frac{3}{2} x \) mit \(k≠ 0\) liegen.
k=1
\( f_{k}(x)=\frac{1}{6 } \cdot x^{3}-x^{2}+\frac{3}{2} x \)
\( f'_{1}(x)=\frac{1}{2 } \cdot x^{2}-2x+\frac{3}{2} \)
\( \frac{1}{2 } \cdot x^{2}-2x+\frac{3}{2}=0 \)
\( x_1=1 \)
\( f_{1}(1)=\frac{1}{6 }-1+\frac{3}{2} =\frac{2}{3} \)
Art des Extremum:
\( f''_{1}(x)= x-2 \)
\( f''_{1}(1)= 1-2<0 \) Maximum
k=-1
\( f_{-1}(x)=-\frac{1}{6 } \cdot x^{3}-x^{2}+\frac{3}{2} x \)
\( f'_{1}(x)=-\frac{1}{2 } \cdot x^{2}-2x+\frac{3}{2} \)
\( -\frac{1}{2 } \cdot x^{2}-2x+\frac{3}{2} =0 \)
\( x=\sqrt{7}-2 \)
\( f_{-1}(\sqrt{7}-2)\\=-\frac{1}{6 } \cdot (\sqrt{7}-2)^{3}-(\sqrt{7}-2)^{2}+\frac{3}{2} (\sqrt{7}-2)\\ =\frac{1}{3} (7 \sqrt{7}- 17)≈0,51\)
k=2
\( f_{2}(x)=\frac{1}{12 } \cdot x^{3}-x^{2}+\frac{3}{2} x \)
\( f'_{2}(x)=\frac{1}{4 } \cdot x^{2}-2x+\frac{3}{2} \)
\( \frac{1}{4 } \cdot x^{2}-2x+\frac{3}{2}=0 \)
\(x_1=4-\sqrt{10}\)
\( f_{2}(4-\sqrt{10})\\=\frac{1}{12 } \cdot (4-\sqrt{10})^{3}-(4-\sqrt{10})^{2}+\frac{3}{2} (4-\sqrt{10})\\=\frac{1}{3} (5 \sqrt{10} - 14)≈0,6\)
k=-2
\( f_{-2}(x)=-\frac{1}{12 } \cdot x^{3}-x^{2}+\frac{3}{2} x \)
\( f'_{-2}(x)=-\frac{1}{4 } \cdot x^{2}-2x+\frac{3}{2} \)
\( -\frac{1}{4 } \cdot x^{2}-2x+\frac{3}{2}=0 \)
\(x = \sqrt{22} - 4\)
\( f_{-2}(\sqrt{22} - 4)\\=\frac{1}{12 } \cdot (\sqrt{22} - 4)^{3}-(\sqrt{22} - 4)^{2}+\frac{3}{2} (\sqrt{22} - 4)\\=\frac{2}{3}(23\sqrt{22} - 107)≈0,586\)
k=3
\( f_{3}(x)=\frac{1}{18 } \cdot x^{3}-x^{2}+\frac{3}{2} x \)
\( f'_{3}(x)=\frac{1}{6 } \cdot x^{2}-2x+\frac{3}{2}\)
\(\frac{1}{6 } \cdot x^{2}-2x+\frac{3}{2}=0\)
\(x_1=6-3\cdot \sqrt{3} \)
\( f_{3}((6-3\cdot \sqrt{3} ))\\=\frac{1}{18 } \cdot (6-3\cdot \sqrt{3} )^{3}-(6-3\cdot \sqrt{3} )^{2}+\frac{3}{2} (6-3\cdot \sqrt{3} )\\=9 \sqrt{3}-15≈0,588\)
\(\red{k= \frac{1}{6} }\)
\( f_{\frac{1}{6} }(x)= x^{3}-x^{2}+\frac{3}{2} x \)
Keine Extremstellen
Untersuchung auf Sattelpunkt:
\( f_{k}(x)=\frac{1}{6k } \cdot x^{3}-x^{2}+\frac{3}{2} x \)
\( f'_{k}(x)=\frac{1}{2k } \cdot x^{2}-2x+\frac{3}{2} \)
\( f''_{k}(x)=\frac{2}{2k } \cdot x-2 \)
\(\frac{2}{2k } \cdot x-2=0 \)
\(x=2k \)
\( f'_{k}(2k)=\frac{1}{2k } \cdot (2k)^{2}-2\cdot (2k)+\frac{3}{2} \)
\( \frac{1}{2k } \cdot (2k)^{2}-2\cdot (2k)+\frac{3}{2}=0 \)
\( k=\frac{3}{4} \) \(x=\frac{3}{2} \)
Bei \( k=-\frac{3}{4} \) ist kein Sattelpunkt
Sattelpunktfunktion:
\( s_{k}(x)=\frac{2}{9 } \cdot x^{3}-x^{2}+\frac{3}{2} x \)
Bei \(y=x^3-x^2+1,5x\) gibt es keinen Hochpunkt mehr.
Die grüne Ortslinie für die Hochpunkte ist auch die Ortslinie für die Tiefpunkte. Der schwarze Graph mit \(k=\frac{1}{6}\) hat nun keine Extrema mehr. Darum muss k im Definitionsbereich eingeschränkt werden.