Suche bei dieser Funktion die Hochpunkte und die Ortskurve? ft(x) = x^3-t^2*x+3

Question

Funktionenschar ft(x) = x^3-t^2*x+3

b) Bestimmen Sie die Koordinaten der Hochpunkte von ft sowie die zugehörige Ortskurve.

Answer 1

ft(x) = x^3 - t^2·x + 3

ft'(x) = 3·x^2 - t^2

Extremstellen bei 

ft'(x) = 0

3·x^2 - t^2 = 0
x = ± t/√3

ft(t/√3) = 3 - 2/9√3·t^3

ft(-t/√3) = 3 + 2/9√3·t^3

Ortskurve der Extrempunkte

3·x^2 - t^2 = 0
t = ± √3·x

 

o(x) = x^3 - t^2·x + 3 = x^3 - (± √3·x)^2·x + 3
o(x) = 3 - 2·x^3

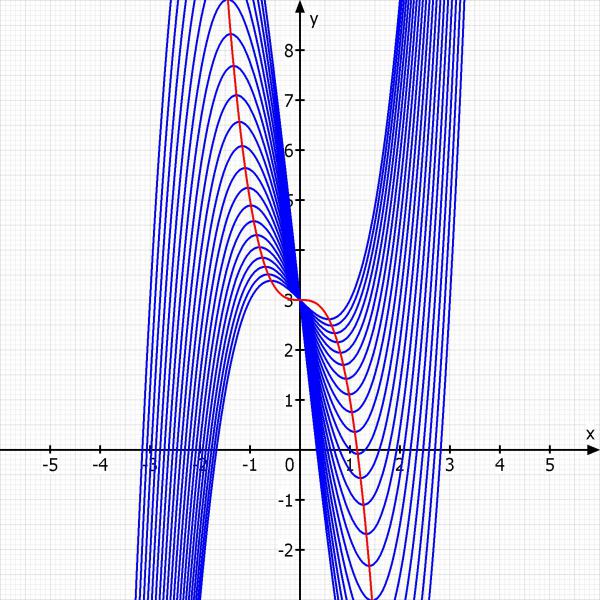
Hier noch eine Skizze:

Comments

Bei der bestimmungdes y-Wertes hab ich ehrlich gesagt noch probleme bei der zusammenfassung.

 

nach dem einsetzen (x-wert) hab ich dann das hier: f(x)=(-√1/3*t)³ - t²* ((1/3)*t)+3

aber das vereinfachen krieg ich irgendwie nie richtig hin ...

---

ft(x) = x³ - t²·x + 3

ft(x) = (t/√3)^3 - t^2·(t/√3) + 3

ft(x) = t^3/(3√3) - t^3/√3 + 3

ft(x) = 1/3*t^3/√3 - 1t^3/√3 + 3

ft(x) = -2/3*t^3/√3 + 3

ft(x) = -2/9*√3*t^3 + 3