Maclaurin Reihe bestimmen

Question

Bestimmen sie die Maclaurin Reihe der folgenden Funktion f (x). Berechnen sie die Funktionswerte an den jeweils angegebenen Punkten x1 unter Verwendung der ersten 2,3 ,4 bzw. 5 Glieder der Reihe und vergleichen Sie mit dem "exakten" Wert.

f(x) = e^x cos (x)  x₁ = 0,2 

Ich hab die Maclaurin Reihe im Internet gegooglet . Brauch ich hier diese?

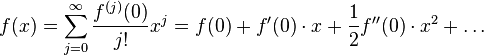
ICh benötige auf jeden Fall die erste Ableitung und die zweite nach dieser Formel

f(x)= e^xcosx → produktregel

f´(x) = e^x cos(x)-sin(x) e^x 

⁼ e^{x (}cos(x) - sin(x))

f´´(x)=  -e^x ((x+1) sin( x) + (x-1) cos(x))

Comments

Na, da wirst Du wohl noch zwei weitere Ableitungen benötigen... warum nimmst Du eigentlich nicht die Definitionen aus deinen Vorlesungsunterlagen? Google ist eine Quelle für Bastler, aber nicht unbedingt für Studenten!

---

warum benötige ich weitere ableitungen ?

wir haben dieses bsp aufbekommen, dazu haben wir noch nichts gerechnet deswegen hab ich google als unterstützung genommen

---

"...unter Verwendung der ersten 2, 3, 4 bzw. 5 Glieder der Reihe"

Also gegen Google habe ich an sich nichts, manchmal benutze ich es sogar selbst! Aber eine Defonition der Maclaurin-Reihe sollten deine Unterlagen schon hergeben. Man tut sich oft leichter, zunächst mit den Mitteln des eigenen Unterrichts zu arbeiten und ggf. weitere Quellen zusätzlich dazu hinzuzuziehen.