Berechne die drei Winkel für a = 6 cm und h = 8 cm (Quadratische Pyramide)

Question

In einer quadratischen Pyramide lassen sich unterschiedliche Winkel finden.

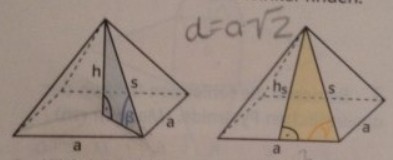
β ... Winkel zwischen Seitenkante und Grundfläche

γ ... Winkel zwischen Seitenkante und Grundkante

a) Berechne die drei Winkel für \( a=6,0 \mathrm{~cm} \) und \( h=8,0 \mathrm{~cm} \).

b) Wie groß ist die Mantelfiäche für \( \mathrm{a}=25,0 \mathrm{~cm} \) und \( \alpha=58,4^{\circ} ? \)

c) Berechne die Oberfläche fur :s \( =27,5 \mathrm{~cm} \) und \( \beta=78,3^{\circ} \).

Answer 1

Einen Winkel braucht man nicht zu berechnen , der ist jeweils schon gekennzeichnet, der rechte Winkel.

Für β braucht man die halbe Diagonale

d/2=6/2 *√2

tan β=8/(3√2).     β=62,06 Grad

für γ braucht man s

s=√(8²+(3√2)²).      s= 9, 05

cosγ=3/ 9,05.          γ=71,59 Grad

Der gesuchte Winkel α (rot)

tanα= 8/3.          α =69,44 Grad

Answer 2

a=6 und h=8 gibt erst mal für die
Bodendiagonale  D = a*√(2)
Im blauen Dreieck ist unten  die halbe
Diagonale   also  (a/2)*√(2)

Dann ist tan(beta) = Gegenkathete / Ankathete 
=  h / (  (a/2)*√(2) )  = 8  /  4,24 = 1,88
also beta = 62Grad

Im blauen Dreieck rechnest du am besten noch s
aus und kannst dann im gelben weiter machen.