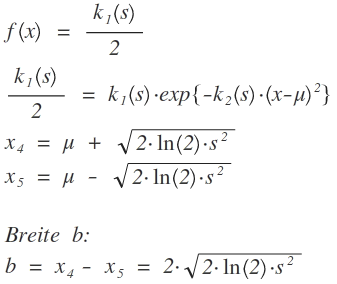Kurvendiskussion
1. Funktion, Graf der Funktion, kurze Beschreibung:
Hier erstmal die
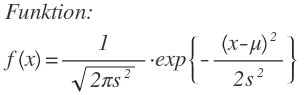
(hoffe sie entspricht auch der, die Du gemeint hast)
Verlauf der Funktion für f(x; s=1,5; μ=0) [flache Kurve], f(x; s=1,0; μ=0), f(x; s=0,5; μ=0) [Spitze Kurve] und f(x; s=0,5; μ=3).
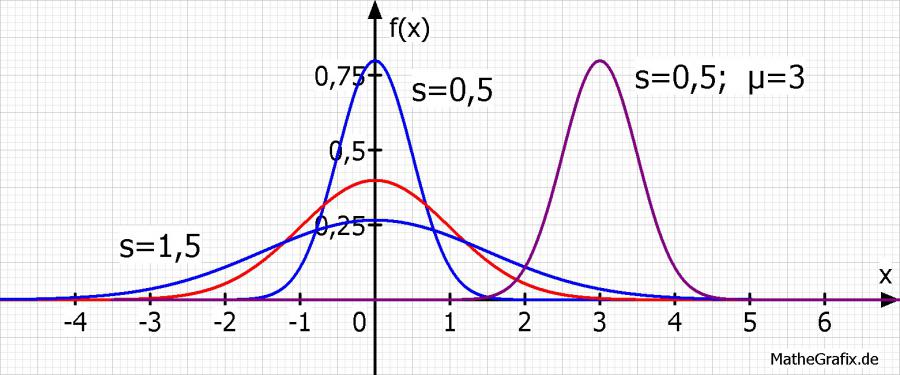
Wie man sieht verschiebt μ die Funktion für positive Werte nach rechts; dem entsprechend wandert sie für negative Werte nach links.
Je kleiner s wird desto höher liegt das Maximum der Funktion.
* Für s→0 geht f(x0)→∞
* Für s→∞ geht f(x0)→0
2. Kürzere Schreibweise der Funktion:
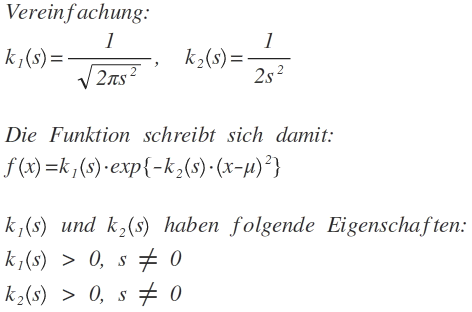
Veranschaulicht:
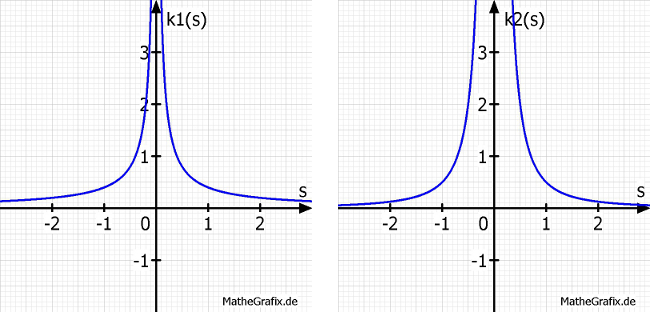
Diese Funktionen werden eingeführt um im Folgenden weniger Schreibaufwand zu haben. Sie können jederzeit wieder ersetzt werden. Die Grafen wurden hinzugefügt um den Einfluss von s abschätzen zu können.
3. Nullstellen:
Um die Nullstellen zu ermitteln muss man die Funktion 0 setzen.
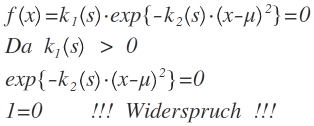
Die Exponentialfunktion kann nicht 0 werden. Damit ergibt sich ein Widerspruch. Die Funktion hat also keine Nullstellen.
(Dies Stimmt mit dem Funktionsverlauf oben in der Zeichnung überein. Sollte also richtig sein.)
4. Weitere Vereinfachung, Ableitungen von f(x):
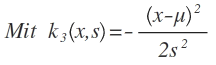
1. Ableitung:
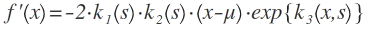
2. Ableitung:
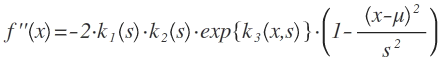
3. Ableitung:
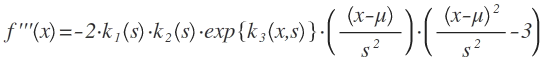
5. Bestimmung der Extrema:
Um die Extrema zu bestimmen muss man die 1. Ableitung 0 setzen (hinreichende Bedingung). Um zu ermitteln ob es ein Maximum, ein Minium oder ein Sattelpunkt (kein Extremum) ist setzt man den erhaltenen x-Wert in die 2. Ableitung ein (notwendige Bedingung).
* Für f''(x1) > 0 ergibt sich ein Minimum
* Für f''(x1) < 0 ergibt sich ein Maximum
* Für f''(x1) = 0 ergibt sich ein Sattelpunkt
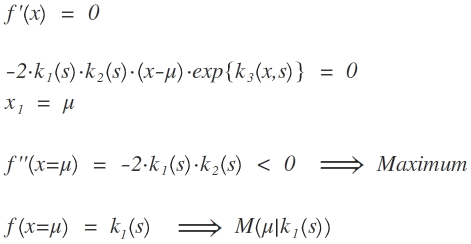
Es gibt also ein Maximum.
6. Bestimmung der Wendepunkte:
Um die x-Werte der Wendepunkte zu bestimmen setzt man die 2. Ableitung 0 (hinreichende Bedingung). Um zu ermitteln ob es sich tatsächlich um einen Wendepunkt handelt, setzt man den zuvor ermittelten Wert in die 3. Ableitung der Funktion ein; ist das Ergebnis =/= 0, dann handelt es sich um einen Wendepunkt (notwendige Bedingung).
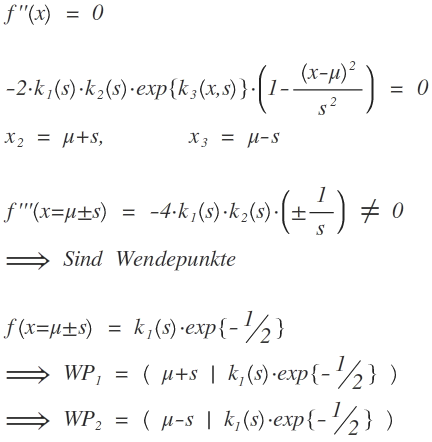
Es gibt also zwei Wendepunkte.
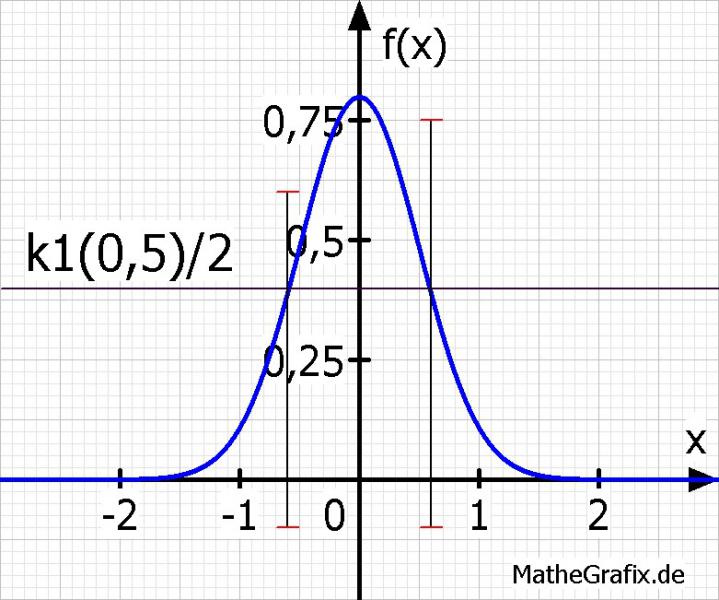
7. Breite auf halber Höhe des Maximums:
Um die die x-Werte für die Breite zu bestimmen setzt man die Funktion mit der halben Höhe des Maximums gleich und berechnet x. Man erhält zwei Werte, bildet die Differenz und erhält so den Abstand. Die Höhe des Maximums ist gleich dem y-Wert des Maximums.