Aufgabe Sandkasten:
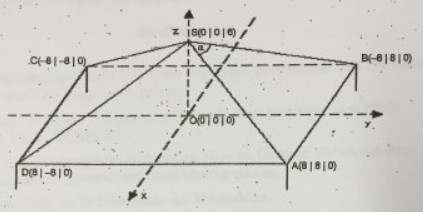
Ein Sandkasten, dessen obere Kanten das Quadrat \( A B C D \) bilden, soll als Schutz vor Verschmutzung einen Holzdeckel in Form einer senkrechten Pyramide mit der Spitze S erhalten (siehe Skizze). \( 1 \mathrm{LE}=1 \mathrm{dm} \).
a) Zuerst werden die vier Seitenflächen des Deckels zugesägt. Berechnen Sie dazu die Länge der Pyramidenkante AS und den Winkel \( \alpha \) zwischen den Kanten \( A S \) und \( B S \).
b) Berechnen Sie, wie viel Quadratmeter Holz für den Bau des Deckels benötigt werden. Der entstehende Abfall sowie Verbindungselemente bleiben unberücksichtigt.
c) Der Sandkasten ist so gefüllt, dass die ebene Sandoberfläche genau die Fläche \( A B C D \) ist. Ein großer Ball mit einem Radius von \( 2,5 ~ \mathrm{dm} \) liegt genau in der Mitte auf der Sandfläche, bezogen auf die obige Skizze also genau auf dem Koordinatenursprung. Geben Sie die Koordinaten des Mittelpunktes des Balls an.
Weisen Sie nach, dass der Ball beim Aufsetzen des Deckels auf den Sandkasten nicht zusammengedrückt wird.
d) Zum Anheben des Deckels wird auf den Seitenkanten AS und CS in gleicher Höhe je ein Haltegriff angebracht.
Erstellen Sie eine Gleichung der Geraden \( g_{A S} \).
Der Befestigungspunkt \( H_{1} \) des Griffs auf \( A S \) soll vom Befestigungspunkt \( H_{2} \) des Griffs auf CS einen Abstand von 4 dm haben. Weisen Sie nach, dass \( H_{1} \) und \( H_{2} \) diesen Abstand haben, wenn sie sich in der Höhe \( z=6-\frac{3 \sqrt{2}}{4} \) befinden.