Aufgabe Arzneimittelkonzentration:
Bei einer Arznei, z.B. einer Tablette, steht die Wirkung (z.B. Schmerzlinderung o.ä.) in direktem Zusammenhang mit der Konzentration des in der Arznei enthaltenen Wirkstoffes im Blut, d.h., bei hoher Konzentration des Wirkstoffes verspürt der Patient eine intensive Wirkung. Die Konzentration des Wirkstoffes im Blut wird in \( \mu \mathrm{g} \) pro Liter angegeben.
Die nachfolgende Graphik zeigt die Änderungsrate der Konzentration in \( \mu \mathrm{g} \) pro Liter je Stunde in Abhängigkeit von der Zeit \( t \) in h.
Dabei ist t die Zeit in \( \mathrm{h} \) seit Beginn der Einnahme \( (\mathrm{t}=0 \) ).
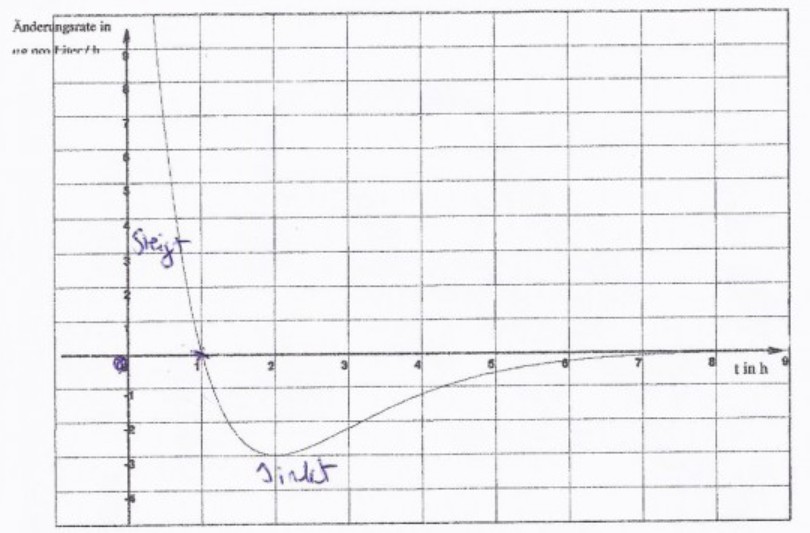
a) Geben Sie die Zeitintervalle an, in denen die Wirksamkeit zunimmt und die Zeitintervalle, in denen die Wirksamkeit abnimmt. Begründen Sie Ihre Aussagen.
b) Bestimmen Sie, zu welchem Zeitpunkt die Konzentration des Wirkstoffes am größten ist und begründen Sie Ihr Ergebnis.
c) Bestimmen Sie, zu welchem Zeitpunkt die Abnahme der Konzentration am größten ist und begründen Sie Ihr Ergebnis.
d) Die Wirksamkeit der Arznei wird durch die Funktion f mit der Funktionsgleichung
\( f(t)=3 t \cdot e^{2-t} ; \quad t \geq 0 \)
beschrieben. Dabei beschreibt \( \mathrm{f}(\mathrm{t}) \) die Konzentration des Wirkstoffes im Blut (gemessen in \( \mu \) g pro Liter) zur Zeit t (gemessen in h seit der Einnahme). Weisen Sie unter Verwendung von f rechnerisch nach, dass Ihr Ergebnis aus Teilaufgabe b korrekt ist. (Falls Sie b nicht gelöst haben, berechnen Sie nun den in b gesuchten Zeitpunkt). Berechnen Sie auch die Höhe der Konzentration zu diesem Zeitpunkt.
e) Begründen Sie, dass das Vorzeichen von \( \mathrm{f} \) ' durch den Term \( 3 - 3 \mathrm{t} \) bestimmt wird, und erklären Sie mit Hilfe dieser Aussage nachträglich den Verlauf des abgebildeten Graphen.
f) Beschreiben Sie den zeitlichen Verlauf der Wirksamkeit der Arznei.