Extremstellen bei f(x)=x^4-4x^2

Question

,

ich habe ein Problem mit dieser uAfgabe und weiß einfach nicht wie und was ich jetzt machen muss:

gegebene Funktion: f(x)=x^4-4x^2

Ich muss Nullstellen, Hoch-, Tief-, und Wendepukte berechnen.

WIeso ist der Graph symmetrisch zur y-Achse?

Vielen Danke schon mal im Voraus :)

Answer 1

gegebene Funktion: f(x)=x⁴-4x²

Ich muss Nullstellen, 

0 =x⁴-4x² nach x auflösen.
0 = x^2 ( x^2 - 4) = x^2 (x+2)*(x-2)
Nullstellen x1 = -2, x2 = 0 (Doppelte Nullstelle und daher gleichzeitig Extremalstelle) und x3 = 2.

Hoch-, Tief-, und 

f '(x) = 4x^3 - 8x 

 4x^3 - 8x = 0 nach x auflösen
4x (x^2 - 2) = 0
4x ( x -√2)* (x+√2) = 0
Extremalstellen: x1 = 0, x2 = -√2 und x3 = √2
Extremalpunkte P(0,0) . Q( -√2 , (-√2)⁴-4(-√2)² ) = Q(-√2 , 4 - 8) = Q ( -√2, -4) und R(√2, -4)  Da sich Hoch- und Tiefpunkte abwechseln müssen bei Polynomen: P ist Hochpunkt und Q und R sind Tiefpunkte.

Wendepukte berechnen.

f ''(x) = 12x^2 - 8

12x^2 - 8 = 0 nach x auflösen.

12x^2 = 8

x^2 = ± 8/12 = ± 2/3

W1(2/3, (2/3)⁴-4 (2/3) ² ) = W1(2/3, 16/81 - 16/ 9) = W1(2/3, -128 / 81)

W2(-2/3, -128/81)

WIeso ist der Graph symmetrisch zur y-Achse?

 f(x)=x⁴-4x² 

 f(-x)=(-x)⁴-4(-x)² =x⁴-4x² = f(x) q.e.d. für "achsensymmetrisch zur y-Achse"

 Rechnungen: (Bitte selbst nachrechnen und Korrekturen melden)

Answer 2

Hi,

bilde dir mal zunächst die ersten 3 Ableitungen ;) 

Ableitungen

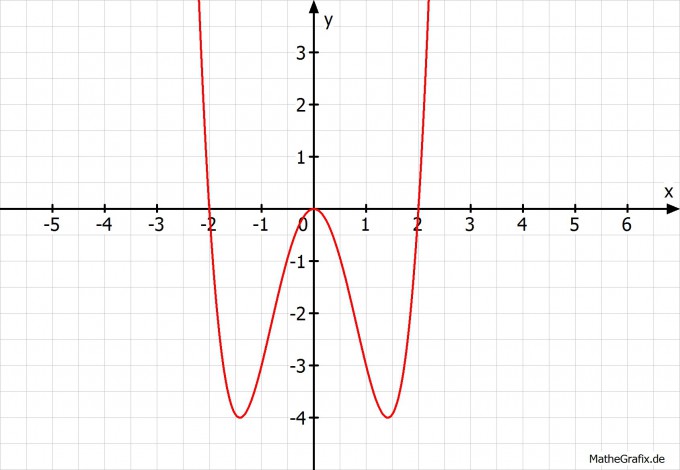
f(x)= x⁴-4x²

f'(x)= 4x³-8x

f''(x)= 12x²-8

Nullstellen

Um die Nullstellen zu berechnen, musst Du ja die Funktion gleich Null setzen und einfach nach x auflösen und das machen wir mal

x⁴-4x²=0

x₁= 0

x₂=-2

x₃=2

Also lauten deine Nullstellen N₁(0|0), N₂(2|0) und N₃(-2|0)

Extrema

Setze mal zunächst die 1. Ableitung gleich Null und löse nach x auf ;)

4x³-8x=0 

x₁=0

x₂=-√2

x₃=√2

Nun setzt Du das mal in die 2. Ableitung ein, also f''(x₀) und schaust Dir die Bedinung an ;)

f''(x₀)<0 Hochpunkt

f''(x₀)>0 Tiefpunkt

f''(0)= 12*0²-8= -8 H(0|0)

und so machst Du weiter

Wendepunkte

Setze die zweite Ableitung gleich Null und löse nach x auf ;)

und die Bedinung für ein Wendepunkt ist f'''(x₀)≠0

Hier nochmal die Grafik deiner Funktion:

Alles klar?