Flächeninhalt in Polarkoordinaten

Question

Aufgabe (Flächeninhalt in Polarkoordinaten):

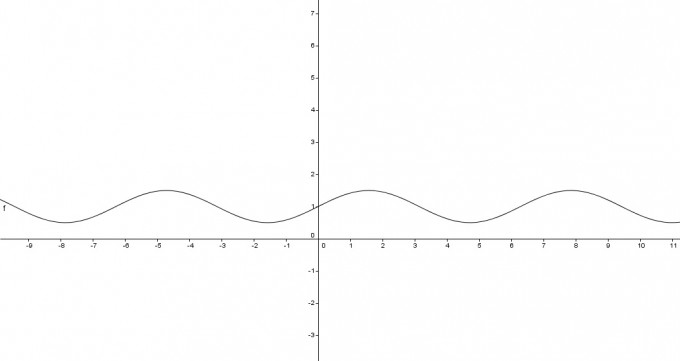
Welche Kurve ist durch \( r=1+\frac{1}{2} \sin (\theta), 0 \leq \theta \leq 2 \pi \) (in Polarkoordinaten) gegeben?

Machen Sie eine Skizze der Kurve.

Berechnen Sie den Flächeninhalt, den die Kurve fiur \( 0 \leq \theta \leq 2 \pi \) einschließt.

Tipp: \( \int \sin ^{2}(x) d x=\frac{1}{2} x-\frac{1}{2} \sin (x) \cos (x)+c \)

Answer 1

Hi,

zuerst einmal wie die Kurve im kartesischen Koordinatensystem aussehn würde:

https://www.wolframalpha.com/input/?i=polar+plot+r%3D1%2B1%2F2sin+theta

den Flächeninhalt in Polarkoordinaten berechnest du mit dem Doppelintegral:

$$ \int \limits_0^{2\pi} \int \limits_0^{r(\theta)}r drd\theta = \int \limits_0^{2\pi}\frac{1}{2}[r(\theta)]^2d\theta$$

und \( r(\theta) = 1 + \frac{1}{2} sin( \theta) \).

Gruß

Comments

Danke aber ich komme genau bei den Doppelintegralen nicht weiter. Wäre sehr nett, wenn sie mir die Rechnung senden könnten.

---

Teile das Integral in einzelne Summanden auf und verwende den Hinweis in der Aufgabenstellung.

Alternativ schreibe an welcher Stelle genau du nicht weiter kommst.