Wie heißen die beiden Nullstellen rechnerisch/zeichnerisch)? Bsp. y =x² +x - 0,5

Question

Ich habe irgendeine schwere Aufgabe zu lösen für die Schule:

Man soll die Nullstellen berechnen und zeichnerisch bestimmen.

1.   y= x² - 4x +3

2.  y =x² +x - 0,5

Bitte mit Erklärung, Rechenweg damit ich das verstehe.

Answer 1

Zeichnerisch bestimmen funktioniert so, dass Du Dir die Funktionen erstmal malst und die Schnittstellen mit der x-Achse bestimmst.

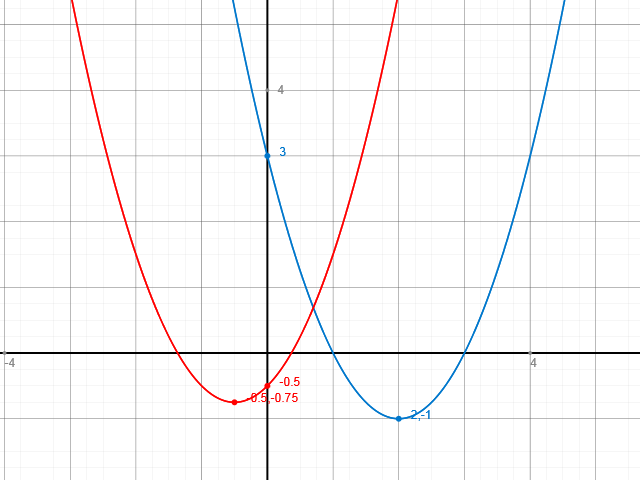
Der blaue Graph entspricht dabei Deiner ersten Funktion. Die Nullstellen sind mit x=1 und x=3 recht gut ablesbar.

Beim roten Graph erschwert sich das ganze, da wir keine ganzzahligen Nullstellen haben.

Man kann die Nullstellen bei etwa x=-1.4 und x=0.4 vermuten.

 

Zur Rechnung: Es gibt viele Möglichkeiten des bestimmens.

Blauer Graph (pq-Formel):
Hier solltest Du die pq-Formel kennen. Wende sie an, wobei p=-4 und q=3.
Was erhältst Du? Zur Kontrolle (siehe auch oben) x₁=1 und x₂=3

 

Roter Graph (quadratische Ergänzung):
Neben der pq-Formel gibt es auch die quadratische Ergänzung:

y =x² +x - 0,5=0       |erkennen, dass sich ein Binom bildet aus (x+0,5)²=x²+x+0,25

x² +x +0,25 -0,25 - 0,5=0

(x+0,5)²-0,75=0                   |+0,75

(x+0,5)²=0,75                      | Wurzel ziehen. Vorsicht wegen Vorzeichen!

x+0,5=±√(0,75)                   |-0,5

x=-0,5±√(0,75)

 

x₁≈-1,366

x₂≈0,366

 

 

Klar? ;)

 

Answer 2

1.   y= x² - 4x +3

Für die Nullstellen musst du x^2 - 4x + 3 = 0 lösen.

Hier kann man faktorisieren, da 3 = 3*1 und - 4 = - 1 -3. Das geht schneller, als einsetzen in die Formel.

(x-3)(x-1) =0

Nullstellen x1 = 3 und x2 = 1

2.  x² +x - 0,5 = 0

Ich nehme hier die abc-Formel mit a=1, b=1 und c = -0.5

x1,2 = 1/2 (-1 ± √(1 + 2)) = 1/2 (-1 ± √3)

x1,2 = -0.5 ± 0.5* √3

x1 = 0.366025

x2 = -1.366025

Hier noch die Graphen mit den Scheitelpunkten bei (2|-1) für 1. und (-0.5|-0.75) für 2.

 

Comments

Hey Lu,

 

Du hast Dich vertippt x₂≈-1,366  (siehe auch Schaubild oder Deine pq-Formel).

 

Grüße

---

Da spuckt der TR aber wilde Werte aus ;).

Das passt leider weiterhin nicht. x₂≈-1,366.

Siehe wie gesagt auch Dein Schaubild.