Winkel an einem Viereck mit unterschiedlichen Seitenlängen berechnen

Question

Hallo ich suche den Winkel b von folgendem Gebilde.

Gegeben sind Winkel a und c sowie alle vier Seitenlängen A, B, C und D (alle unterschiedlich Lang). Habe es mit dem Sinussatz versucht, bin aber nicht weitergekommen.

hier nocheinmal zur besseren Verständnis die überarbeitete Verion der Frage:

ich suche den Winkel Wab oder Wac von folgendem Gebilde.

Gegeben sind Winkel Wae und Wde sowie alle vier Seitenlängen A, B, C und D

Bild MathematikOCRπ↻
(alle unterschiedlich Lang). Wobei der Wertebereich der genannten gegebenen Winkel innerhalb der gegebenen Werte variieren können.

Habe es mit dem Sinussatz versucht, bin aber nicht weitergekommen.

Hier meine Formel:

Wac=asin((B*sin(Wab)+D*sin(Wae-Wde))/C)

In meiner Formel ist Wac und Wab unbekannt, dafür kommt die bekannte größe A nicht vor. Ich denke ein experte kann mir so eine ähnliche Formel geben bei der nur Wab oder Wac als einziger unbekannter vorkommt.

Comments

hier nocheinmal zur besseren Verständnis die überarbeitete Verion der Frage:

ich suche den Winkel Wab oder Wac von folgendem Gebilde.

Gegeben sind Winkel Wae und Wde sowie alle vier Seitenlängen A, B, C und D (alle unterschiedlich Lang). Wobei der Wertebereich der genannten gegebenen Winkel innerhalb der gegebenen Werte variieren können.

Habe es mit dem Sinussatz versucht, bin aber nicht weitergekommen.

Hier meine Formel:

Wac=asin((B*sin(Wab)+D*sin(Wae-Wde))/C)

In meiner Formel ist Wac und Wab unbekannt, dafür kommt die bekannte größe A nicht vor. Ich denke ein experte kann mir so eine ähnliche Formel geben bei der nur Wab oder Wac als einziger unbekannter vorkommt.

---

Dies Aufgabe ist jetzt gut beschrieben.

Answer 1

Ich denke ich habs.

Den unteren Punkt habe ich mit  P1 bezeichnet.
Den Punkt der mit der Strecke B verbunden wird P2.


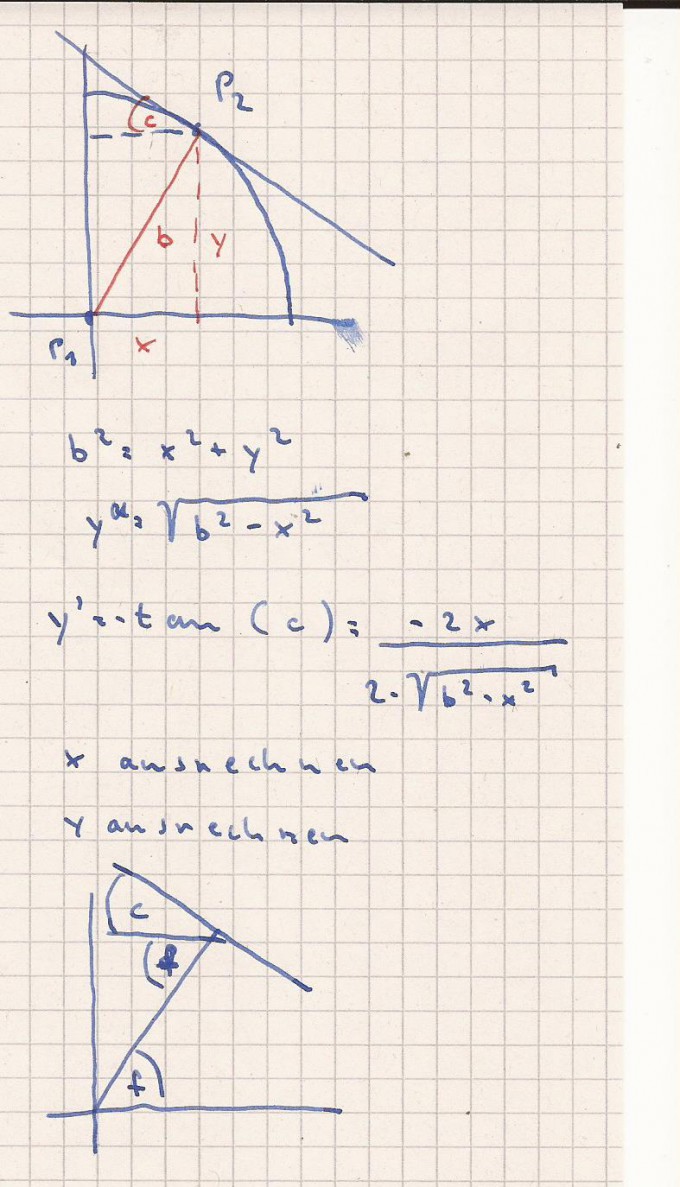
Punkt P1 lege ich den Ursprung eines Koordinatensystems und
schlage einen Kreis mit dem Radius B darum.

Die Strecke D dürfte eine Tangente im Punkt P2 sein.

Für den Kreis ergibt sich die Funktion
y = f ( x ) = √ ( B^2 - x^2 )
1.Ableitung bilde
f ´ ( x ) =  2x /  [ 2 * √ ( B^2 - x^2 ) ]
f ´( x ) ist die Steigung im Punkt P2 und ist = tan ( Winkel c )
tan ( Winkel c ) = 2x /  [ 2 * √ ( B^2 - x^2 ) ]
Damit kann x ausgerechnet und dann y.
Über y / x kann der Winkel f ausgerechnet werden und
damit der Winkel Wbd.

Ich denke dies ist der Einstieg und alles übrige kann auch
berechnet werden.

Gib einmal ein Beispiel A,B,C,D, Wae, Wde.
Oder auch nur B, Wde.

mfg Georg

Comments

Das ging aber schnell!

Zeichnerisch ermittelte Werte:

A= 186,55mm

B= 125mm

C:= 203mm

D= 90mm

Wae = 15,2°

Wde = 32,7°

Die Lösung (zeichnerisch)

Wab=109,3°

Was ich aber in Wirklichkeit suche ist Wbe = Wab+Wae

---

Ich gehe jetzt erst einmal einkaufen.
Danach gehts weiter.

---

ich habe inzwischen Ihre Formel nach x umgestellt:

x = C7a tan(c) / Wurzel(1 + tan(c)^2)

mit x und b bekomme ich mit hilfe des rechtwinkeligen Dreieck den winkel f

f = acos(Ankathede/Hypodenuse) = acos (x/b) = acos (tan(c) / Wurzel(1 + tan(c)^2) )

Die Summe der Winkel c + f ist aber immer 90°, Oder habe ich ein Rechenfehler gemacht? denn dieser darf nicht immer 90° sein.

---

Genau das ist mir auch aufgefallen. Da ich angenommen habe
D wäre eine Tangente an den Kreis mit Radius B. Dann ist der Winkel
immer 90 ° und nicht mehr flexibel.
Ich melde mich wieder.

---

Wab=109,3°
Wae = 15.2 °
Was ich aber in Wirklichkeit suche ist Wbe = Wab+Wae

Müßte ja 109.3 + 15.2 = 124.5 ° sein.

Wenn der erste Winkel ermittelt ist kann auch alles andere berechnet werden.

Ich kann den Winkel wab jetzt rechnerisch ermitteln.

Das Ganze habe ich jetzt in Form eines ersten Computerprogramms
( DOS ) vorliegen. Entweder ich feile jetzt noch daran herum damit Sie
auch damit arbeiten können oder es gelingt mir das Ganze in einem
( manuellen ) Rechenvorgang unterzubringen.

Die ganze Berechnung war / ist nicht trivial.

Sie brauchen nur das Rechenergebnis für Wae ?

---

Stimmt ist 109.3 + 15.2 = 124.5 °

Wobei 15,2 ja gegeben ist. Also ist die 109,3 bzw. Wab gesucht.

Ein C - Code wäre auch hilfreich.

---

Der Code in Borland-Pascal kann auch zur Verfügung gestellt werden.

Eine Formel habe ich noch nicht herausgefunden. Es ist vielleicht möglich das es diese gibt.

uses crt ;

const ddt = 0.01 ;

var wae,wde : real ;
    a,b,c,d : real ;
    waeb, wdeb : real ;
    yk2,xk1 : real ;
    dx,dy : real ;
    al : real ;
    alb : real ;
    ddx,x1,y1,x2,y2,y22 : real ;
    diff, diffo : real ;


function bogenmass ( x : real ) : real ;
begin
bogenmass:= x * 2.0 * PI / 360.0
end;

procedure kreis1 ;

begin
y1:= sqrt( sqr(b) - sqr( x1 - xk1) )
end;

procedure kreis2 ;

begin
y2:= sqrt( sqr(c) - sqr(x2) ) + yk2;
end;

procedure unter ;

begin
al := al + ddt ;
alb:=bogenmass(al);
ddx := cos(alb) * b;
x1:= xk1 - ddx;
kreis1 ;
x2:= x1 - dx;
y22:= y1+ dy;
kreis2;
diff:= y22-y2;
end;

function bedingung : boolean ;

begin
if diffo > 0 then
  begin
  bedingung := diff < 0 ;
  end
else
  begin
  bedingung := diff > 0 ;
  end;
end;

begin
clrscr;
writeln;
writeln;
writeln('Viereck');
writeln;writeln;
writeln('Dezimal-Punkt bei den Zahlen verwenden z.B. 23.45');
writeln;writeln;
write('L„nge A : ');
readln(a);writeln;
write('L„nge B : ');
readln(b);writeln;
write('L„nge C : ');
readln(c);writeln;
write('L„nge D : ');
readln(d);writeln;
write('Winkel Wae : ');
readln(wae);
writeln;
write('Winkel Wde : ');
readln(wde);
writeln;
{
a:=186.55;
b:=125;
c:=203;
d:=90;
wae:=15.2;
wde:=32.7;
}
waeb:= bogenmass(wae);
wdeb:= bogenmass(wde);
yk2:= sin(waeb) * a;
xk1:= sqrt(sqr(a) - sqr(yk2) );
dy:= d * sin(wdeb);
dx := sqrt(sqr(d) -sqr(dy));
writeln;
al:=wae;
unter ;
diffo:=diff;
repeat;
diffo:=diff;
unter;
until bedingung ;
al:= al - ddt/2.0 ;
writeln('Wbe ',al:7:2,' ø') ;
writeln;
writeln('Beenden mit <RETURN> ') ;
readln;
end.