Aufgabe
Wir sollen zeigen, dass alpha plus beta durch 2 gleich gamma ist
Problem/Ansatz:
Irgendwo bauen wir einen Fehler ein und wir können nicht erkennen wo, wäre schön, wenn uns jemand helfen könnte.
(S. Bilder)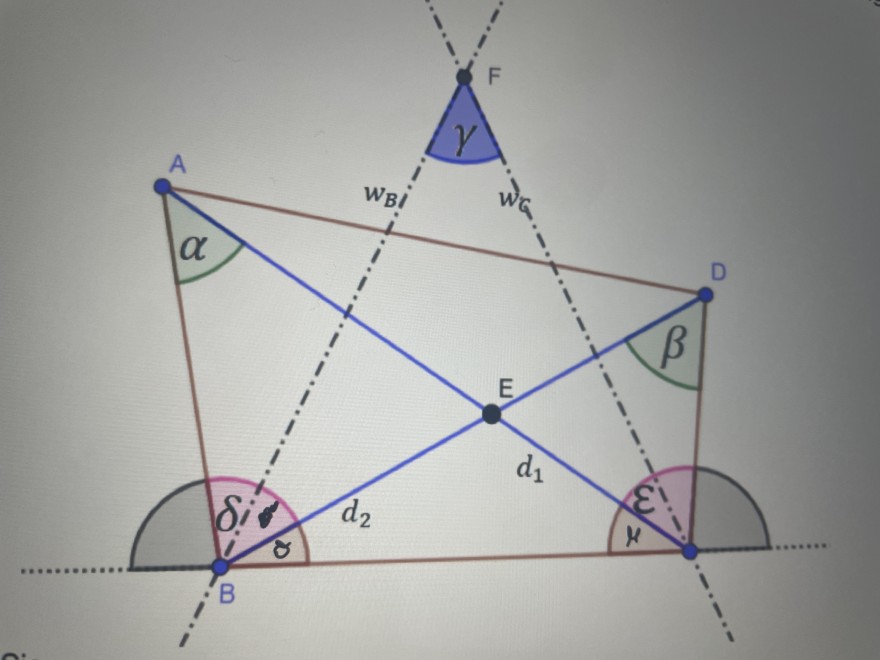
Text erkannt:
180∘−(δ−σ−μ)+180∘−(ε−μ−σ)2180∘−δ+σ+μ+180∘−ε+μ+σ=180∘−(δ2+σ)2−(ε2+μ)y=180∘−δ2−σ−εo^−μ \begin{array}{l}\frac{180^{\circ}-(\delta-\sigma-\mu)+180^{\circ}-(\varepsilon-\mu-\sigma)}{2} \\ 180^{\circ}-\delta+\sigma+\mu+180^{\circ}-\varepsilon+\mu+\sigma \\ =180^{\circ}-\left(\frac{\delta}{2}+\sigma\right)^{2}-\left(\frac{\varepsilon}{2}+\mu\right) \\ y=180^{\circ}-\frac{\delta}{2}-\sigma-\frac{\varepsilon}{\hat{o}}-\mu \\\end{array} 2180∘−(δ−σ−μ)+180∘−(ε−μ−σ)180∘−δ+σ+μ+180∘−ε+μ+σ=180∘−(2δ+σ)2−(2ε+μ)y=180∘−2δ−σ−o^ε−μ
Sind die grau unterlegten Winkel gleichgroß?
Da es nicht angemerkt worden ist, denke ich nein bzw. Irrelevant für die Aufgabe.
Ohne zusätzliche Angaben über den Zusammenhang zwischen dem Dreieck BCF und dem Viereck ABCD ist die Aufgabe nicht lösbar.
Man weiß nur weiter, dass wb die Winkelhalbierende von Delta ist und wc die Winkelhalbierende von epsilon ist.
Die Klammern in der ersten Zeile sind zu streichen.
Danke, das war mein Fehler
γ=180°−δ2−σ−ε2−μμ=180°−σ−∠BEC ⟹ γ=180°−δ2−σ−ε2−(180°−σ−∠BEC)=180°−δ2−σ−ε2−180°+σ+∠BEC=−δ2−ε2+∠BEC∠BEC=180°−∠AEB ⟹ γ=−δ2−ε2+180°−∠AEB∠AEB=180°−δ−α ⟹ γ=−δ2−ε2+180°−(180°−δ−α)=−δ2−ε2+180°−180°+δ+α=δ2−ε2+αε=180°−∠CED−β ⟹ γ=δ2−180°−∠CED−β2+α=δ2−90°+∠CED2+β2+αδ=180°−∠AEB−α ⟹ γ=180°−∠AEB−α2−90°+∠CED2+β2+α=90°−∠AEB2−α2−90°+∠CED2+β2+α=−∠AEB2+∠CED2+β2+α2∠AEB=∠CED ⟹ γ=−∠CED2+∠CED2+β2+α2=β2+α2=α+β2\begin{aligned}\gamma & =180°-\frac{\delta}{2}-\sigma-\frac{\varepsilon}{2}-\mu\\\\\mu & =180°-\sigma-\angle BEC\\\implies\gamma & =180°-\frac{\delta}{2}-\sigma-\frac{\varepsilon}{2}-\left(180°-\sigma-\angle BEC\right)\\ & =180°-\frac{\delta}{2}-\sigma-\frac{\varepsilon}{2}-180°+\sigma+\angle BEC\\ & =-\frac{\delta}{2}-\frac{\varepsilon}{2}+\angle BEC\\\\\angle BEC & =180°-\angle AEB\\\implies\gamma & =-\frac{\delta}{2}-\frac{\varepsilon}{2}+180°-\angle AEB\\\\\angle AEB & =180°-\delta-\alpha\\\implies\gamma & =-\frac{\delta}{2}-\frac{\varepsilon}{2}+180°-\left(180°-\delta-\alpha\right)\\ & =-\frac{\delta}{2}-\frac{\varepsilon}{2}+180°-180°+\delta+\alpha\\ & =\frac{\delta}{2}-\frac{\varepsilon}{2}+\alpha\\\\\varepsilon & =180°-\angle CED-\beta\\\implies\gamma & =\frac{\delta}{2}-\frac{180°-\angle CED-\beta}{2}+\alpha\\ & =\frac{\delta}{2}-90°+\frac{\angle CED}{2}+\frac{\beta}{2}+\alpha\\\\\delta & =180°-\angle AEB-\alpha\\\implies\gamma & =\frac{180°-\angle AEB-\alpha}{2}-90°+\frac{\angle CED}{2}+\frac{\beta}{2}+\alpha\\ & =90°-\frac{\angle AEB}{2}-\frac{\alpha}{2}-90°+\frac{\angle CED}{2}+\frac{\beta}{2}+\alpha\\ & =-\frac{\angle AEB}{2}+\frac{\angle CED}{2}+\frac{\beta}{2}+\frac{\alpha}{2}\\\\\angle AEB & =\angle CED\\\implies\gamma & =-\frac{\angle CED}{2}+\frac{\angle CED}{2}+\frac{\beta}{2}+\frac{\alpha}{2}\\ & =\frac{\beta}{2}+\frac{\alpha}{2}\\ & =\frac{\alpha+\beta}{2}\end{aligned}γμ⟹γ∠BEC⟹γ∠AEB⟹γε⟹γδ⟹γ∠AEB⟹γ=180°−2δ−σ−2ε−μ=180°−σ−∠BEC=180°−2δ−σ−2ε−(180°−σ−∠BEC)=180°−2δ−σ−2ε−180°+σ+∠BEC=−2δ−2ε+∠BEC=180°−∠AEB=−2δ−2ε+180°−∠AEB=180°−δ−α=−2δ−2ε+180°−(180°−δ−α)=−2δ−2ε+180°−180°+δ+α=2δ−2ε+α=180°−∠CED−β=2δ−2180°−∠CED−β+α=2δ−90°+2∠CED+2β+α=180°−∠AEB−α=2180°−∠AEB−α−90°+2∠CED+2β+α=90°−2∠AEB−2α−90°+2∠CED+2β+α=−2∠AEB+2∠CED+2β+2α=∠CED=−2∠CED+2∠CED+2β+2α=2β+2α=2α+β
γ=180∘−0,5δ−σ−μ−0,5ε\gamma=180^\circ-0,5\delta-\sigma-\mu-0,5\varepsilonγ=180∘−0,5δ−σ−μ−0,5ε
α+β=180∘−δ−σ−μ+180∘−σ−μ−ε=2⋅(180∘−0,5δ−σ−μ−0,5ε)=2⋅γ\alpha+\beta\\=180^\circ-\delta-\sigma-\mu+180^\circ-\sigma-\mu-\varepsilon\\=2\cdot(180^\circ-0,5\delta -\sigma-\mu -0,5\varepsilon)\\=2\cdot\gammaα+β=180∘−δ−σ−μ+180∘−σ−μ−ε=2⋅(180∘−0,5δ−σ−μ−0,5ε)=2⋅γ
⇒γ=α+β2\Rightarrow \gamma =\frac{\alpha+\beta}{2}⇒γ=2α+β
Monty: Griechische Buchstaben sind sowohl unter dem Button x4 \sqrt[4]{x} 4x als auch unter dem Button Sym (beide Buttons findest du in der Kopfzeile deiner Antwort) darstellbar und müssen nicht ausgeschrieben werden.
Hallo Roland,
ich benutze LaTeX\LaTeXLATEX schon seit 1993. ☺
Gestern war es schon etwas spät und ich hatte keine Lust, die Backslashes auf meinem Smartphone zu suchen.
:-)
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
