In einer wissenschaftlichen studie wurde eine bakterienkultur in einem gefäß beobachtet. jede stunde wurde die fläche, die von bakterien bedeckt war, gemessen. die bedeckte fläche kann mithilfe der funktion a modelliert werden:
a(t) = - 0.01·t^3 + 0.1·t^2 + t + 1.5
a'(t) = - 0.03·t^2 + 0.2·t + 1
a''(t) = 0.2 - 0.06·t
(a(t) in cm2 ; t in h. )
a) berechne die größe der von den bakterien bedeckten fläche zu beginn der messung und nach drei bzw. acht stunden.
a(0) = 1.5 cm^2
a(3) = 5.13 cm^2
a(8) = 10.78 cm^2
b) bestimme die mittlere wachstumsgewchwindigkeit der bakterienbesetzen fläche in cm2 /h in den ersten vier stunden der messung.
(a(4) - a(0)) / 4 = 1.24 cm^2/h
c) bestimme grafisch die wachstumsgeschwindigkeit zum zeitpunkt t = 6,5
Ich mache es hier rechnerisch. Du kannst es dann an einer Zeichnung nachvollziehen
a'(6.5) = 1.0325 cm^2/h
d) berechne die gleichung der ableitungsfunktion a´ und skizziere ihren graphen. beschreibe den zusammenhang zwischen a und a´ im kontext.
a'(t) = - 0.03·t^2 + 0.2·t + 1
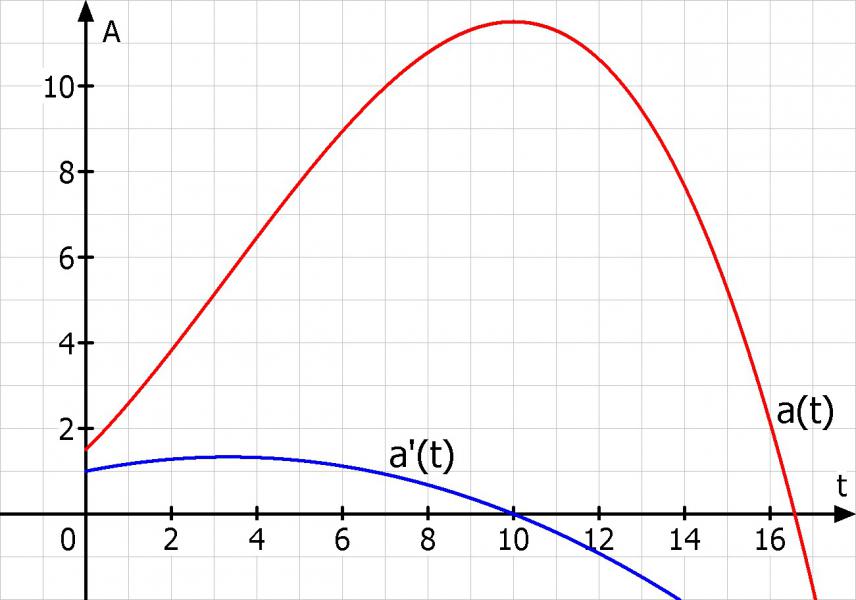
e) entnmm dem graphen der ableitungsfunktion näherungsweise, wann die momentante wachstumsgeschwindigkeit genauso groß war wie zu beginn der beobachtung. wann war sie am größten?
a'(t) = a'(0)
- 0.03·t^2 + 0.2·t + 1 = 1
t = 0 und t = 20/3 ~ 6 h 20 min
a''(t) = 0
0.2 - 0.06·t = 0
t = 10/3 ~ 3 h 20 min