Nullstelle(n) eines komplexen Polynoms und Angabe der Menge

Question

Berechnen Sie die Nullstellen des komplexen Polynoms

\( p(z)=z^{7}+64 z, \quad z \in \mathbb{C} \)

Geben Sie die Menge \( M_{0}:=\{z \in \mathbb{C} \mid p(z)=0 \) und \( \operatorname{Im}(z)>0 \) und \( \operatorname{Re}(z)>0\} \) an.

Ansatz:

Einzige Nullstelle ist 0 ,oder? Und wie gebe ich jetzt die Menge an?

Comments

Das Polynom hat 7 verschiedene Nullstellen.

Answer 1

1. Ausklammern: x * (x^6 + 64)   also x1=0

Die 64 ist eine typisch glatte 2er Potenz: 2^6 = 64, nur dass das mit +64 nicht im Reellen lösbar ist:

x2= 2i

wegen hoch 2 auch die negative:

x3= -2i

Dann Polynomdivision durch (x-2*i)(x+2i) = x²+4  ergibt

= x^4-4*x²+16   

Dafür gibt es 2 Lösungswege:  Spezialfall biquadratische Gleichung oder PQRSTUVW-Formel   

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php   

die letzten 4 Nullstellen:   

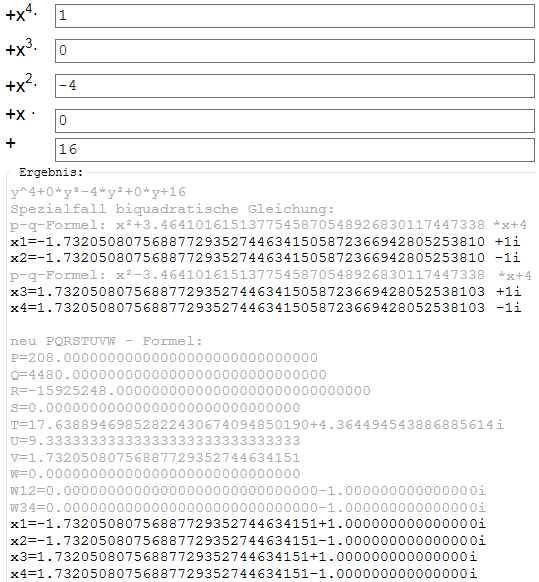
Nun alle weglassen, die Im(z) und Re(z) <=0 sind -> bleiben nur 2 über