Wie groß ist der Flächeninhalt einer Zone der Erde, die zwischen den Breitenkreisen mit φ_{1} = 30°, φ_{2} = 60° nördlicher Breite liegt, und welchen Teil der gesamten Erdoberfläche stellt diese Zone dar?
Die Erde wird genähert als Kugel mit dem Radius r = 6370 km betrachtet.
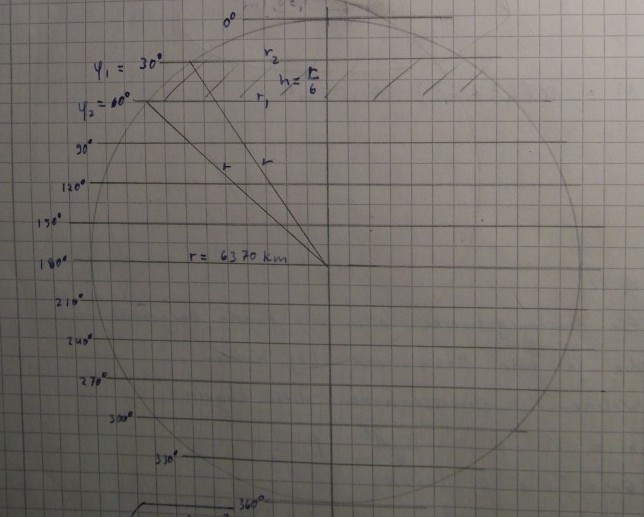
Ansatz/Problem:
Da soll ich ja im Grunde nichts anderes als die Mantelfläche der Kugelzone/-schicht berechnen.
Für die Mantelfläche gilt ja: M = 2*pi*r*h
Die Frage ist, stimmt da meine Höhe mit r/6?
Wenn ja:
M = 2*pi*6370km*(6370km/6)
Im Löser steht da was von:
M = 2*pi*r²*(sin60°-sin30°)
Das ergibt für mich keinen Sinn, weil diese Breitenkreise in Grad ja gar nichts mit einem "Winkel" zu tun haben.