3. Ich verstehe nicht ganz, wo ich selber das gegebene Volumen "eingebaut" habe. Das ist ja notwendig, weil wir das gleiche Volumen behalten möchten.
V = pi·r^2·h
h = v/(pi·r^2)
O = 2·pi·r^2 + 2·pi·r·h = 2·pi·r^2 + 2·pi·r·V/(pi·r^2) = 2·pi·r^2 + 2·V/r
1. Gehe ich recht in der Annahme, dass das Minimieren hier nur deshalb funktioniert, weil unsere Oberflächenfunktion quadratisch und positiv und somit eine nach oben offene Parabel ist?
Die Funktion ist keine Parabel. Sie sieht in etwa wie folgt aus
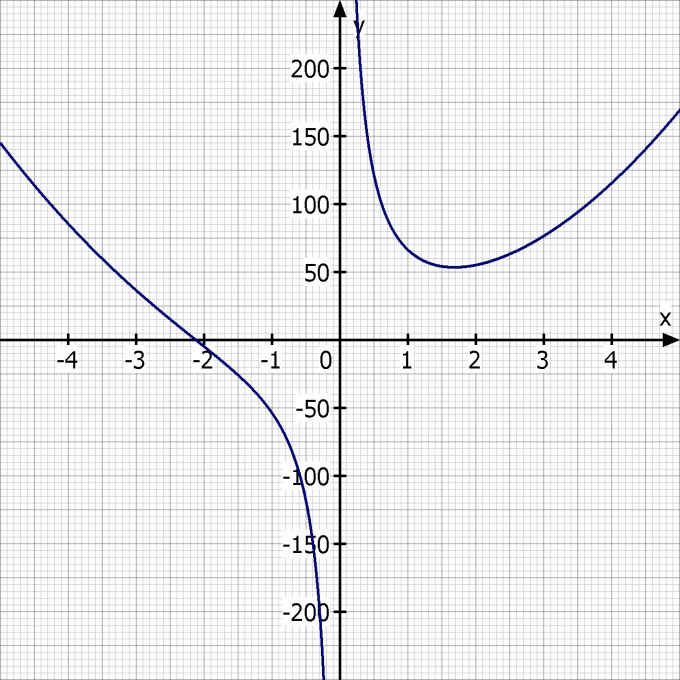
2. Ist es richtig, dass wir bei einer Funktion höheren Grades (zum Beispiel dritten Grades) für eine beliebige, ähnliche Anwendung das Problem hätten, dass mehrere Extremas bestehen können und die Anwendung möglicherweise nicht maximierbar oder minimierbar ist?
Eine Funktion ist eigentlich immer maximier oder minimierbar. Das funktioniert nicht immer algebraisch aber über ein Näherungsverfahren bekommt man eigentlich fast immer eine Lösung.