Viertelkreise in Quadrat: Term für den Flächeninhalt der grau makierten Figur bestimmen.

Question

Aufgabe:

Bestimme einen Term für den Flächeninhalt der grau makierten Figur in Abhängigkeit von a und vereinfache ihn so weit wie möglich.

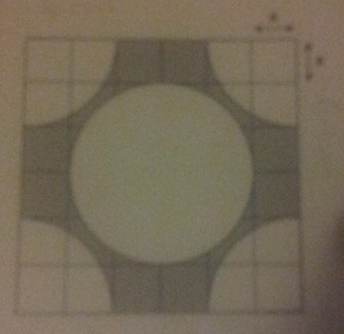
a = 6 cm

Flächeninhalt Quadrat: A = a^2 = 36 cm

Durchmesser des Kreises = 4 cm

Mein Ansatz:

Flächeninhalt Kreis: A = π*d²/4 oder A=π*r²

Flacheninhalt Kreis= 12.56 cm 

Flacheninhallt Viertelkreis: A= r2*π/4= 22*π/4=3.14 cm 

3.14*4 (es gibt vier viertelkreise) =12.56cm 

12.56cm(Flaceninhalt der vier viertelkreise)+12.56 cm (Flacheninhalt des kreises in der mitte)=25.12 cm 

36cm-25.12cm=10.88 cm (das ist der flaechninhakt der Grau makierten Figur)

Ist das so richtig und wenn ja, wie mach ich hieraus einen Term?

Answer 1

a = 6 cm
r = 2 cm

A = Quadrat - 2 * Kreis
A = a^2 - 2 * r^2 * π

vielleicht noch
r = a/3
A = a^2 - 2 * (a/3)^2 * π
A = a^2 - 2 * a/^2 / 9 * π
A = a^2 - ( 1 - 2 / 9  * π )

Answer 2

Das Quadrat hat die Fläche A_(Q) (x) = (6x)^2 = 36x^2

Daraus wird im Ganzen zwei mal ein kleiner Kreis mit Radius r =(2x) ausgeschnitten.

A_(K) (x)= (2x)^2*π = 4x^2 π

Es resultiert

A_(Gesamt) (x) = 36x^2 - 2*4x^2 π

= 36x^2 - 8x^2 π 

= 4x^2 (9 - 2π)

Je nach Anwendung, die nun folgt, ist nun das erste oder zweite Ergebnis geeigneter.

Answer 3

Wird das Quadrat auf die sich hier anbietende Weise in vier kleinere Quadrate zerlegt, so wird auch die graue Figur in vier kongruente graue Teilfiguren zerfallen. Es genügt, die Fläche einer dieser Teilfiguren zu berechnen und zu vervierfachen. Dies führt auf die ganz einfache Rechnung:
$$ A(6) = 4\cdot\left(9-2\pi\right) $$$$ A(a) = 4\cdot\left(9-2\pi\right)\cdot\left(\frac { a }{ 6 }\right)^2 = \frac { 9-2\pi }{ 9 } \cdot a^2 $$