Berechnen Sie ïber dem Dreieck mit den Eckpunkten das Volumen unter der Bildfläche der gegebenen Funktion

Question

Aufgabe (Doppelintegrale in kartesische Koordinaten mit variablen Grenzen):

Berechnen Sie ïber dem Dreieck mit den Eckpunkten \( (0 ; 0),(3 ; 3),(6 ; 0) \) das Volumen unter der Bildfläche der durch \( z=f(x ; y)=x y \) gegebenen Funktion.

Answer 1

Laura,

als erstes solltest du dir eine Zeichnung des Bereiches, über dem integriert werden soll, erstellen. Mit genügend Übung gelingt das auch im Kopf.

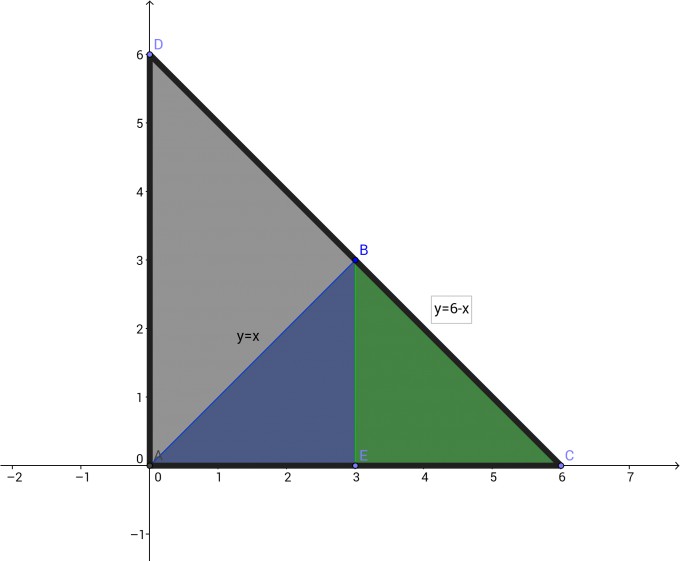
Jetzt kannst du, nachdem du die Grenzen erkannt hast das Volumenintegral aufstellen. Dabei unterteile ich den Bereich in zwei Dreiecke.

$$\color{blue}{\int_0^3 \left(\int_0^x x y \, dy\right) \, dx}+\color{green}{\int_3^6 \left(\int_0^{6-x} x y \, dy\right) \, dx}=\color{blue}{\frac{81}{8}}+\color{green}{\frac{135}{8}}=27$$

Einfacher und kürzer geht es allerdings so:

$$\frac{1}{2}\int_0^6 \left(\int_0^{6-x} x y \, dy\right) \, dx=\frac{54}{2}$$

Warum das funktioniert findest du bestimmt auch heraus. ;)

Comments

danke aber irgendwie komme ich nicht auf das richtige Ergebnis :) MfG

---

letztes bild Klammer richtig setzen bzw. nicht vergessen: Sonst sehe ich auf den ersten Blick keinen weiteren Fehler:

$$-(9*3^2-2*3^3+\frac{1}{8}3^4)$$

---

Nach meiner Rechnung komme ich auf -81 und das ist doch falsch oder? Es muss ja 54/2 rauskommen.

---

$$=\frac{1}{8}3^4+(9*6^2-2*6^3+\frac{1}{8}6^4)-(9*3^2-2*3^3+\frac{1}{8}3^4)=27$$

da beißt die Maus keinen Faden ab

https://www.wolframalpha.com/input/?i=%5Cfrac%7B1%7D%7B8%7D3%5E4%2B%289*6%5E2-2*6%5E3%2B%5Cfrac%7B1%7D%7B8%7D6%5E4%29-%289*3%5E2-2*3%5E3%2B%5Cfrac%7B1%7D%7B8%7D3%5E4%29

---

Danke klappt jetzt alles ich hatte irgendeinen Fehler :)