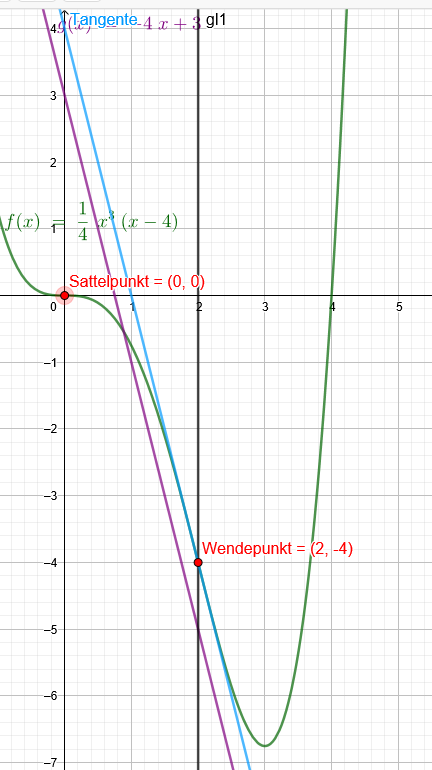
"Gegeben seien die Funktionen \(g(x)= -\frac{3}{4}x^4\) und f(x).
f(x) ist eine Polynomfunktion vierten Grades , die im Ursprung einen Sattelpunkt besitzt. An der Stelle x=2 liegt ein Wendepunkt vor , dessen Tangente parallel zur Geraden \(y=-4x+3\) verläuft."
Nullstellenform der Parabel 4.Grades:
Ursprung ( Sattelpunkt) :
\(f(x)=a*x^3*(x-N)\)
An der Stelle x=2 liegt ein Wendepunkt:
\(f´(x)=a*[3*x^2*(x-N)+x^3*1]\)
\(f´´(x)=a*[6*x*(x-N)+3*x^2*1 +3x^2]\)
\(f´´(2)=a*[6*2*(2-N)+3*2^2 +3*2^2]\)
\(f´´(2)=a*[12*(2-N)+24]\)
\(f´´(2)=0\)
\(a*[12*(2-N)+24=0]\)
\(a*[(2-N)+2=0→N=4]\)
Tangente parallel zur Geraden \(y=-4x+3\) beim Wendepunkt:
\(f´(x)=a*[3*x^2*(x-4)+x^3]\)
\(f´(2)=a*[3*2^2*(2-4)+2^3=-16]\)
\(-16a=-4→a=\frac{1}{4}]\)
\(f(x)=\frac{1}{4}*x^3*(x-4)\)