Kabeldurchmesser, wenn vier gleich große Kabelstränge in einem Rohr untergebracht werden sollen?

Question

Aufgabe:

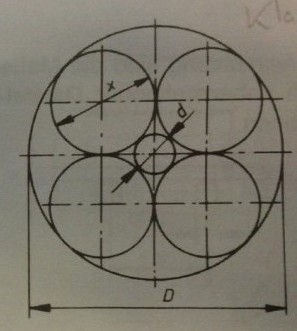
Wie groß darf der Kabeldurchmesser \( \mathrm{x} \) höchstens sein, wenn vier gleich große Kabelstränge in einem Rohr vom Innendurchmesser D untergebracht werden sollen?

a) Berechnen Sie \( x \) in Abhängigkeit von D.

b) Berechnen Sie \( x \) in Abhängigkeit von \( \mathrm{d} \).

Lösungen:

a) \( x=D(\sqrt{2}-1) \)

b) \( x=d(1+\sqrt{2}) \)

Wie sieht der Rechenweg aus?

Answer 1

Ansatz:

D/2 = √((x/2)^2 + (x/2)^2) + x/2

Lösung:

x = D·(√2 - 1)

Ansatz:

d/2 = √((x/2)^2 + (x/2)^2) - x/2

Lösung:

x = d·(√2 + 1)