Funktionsterm, Flächeninhalt

Question

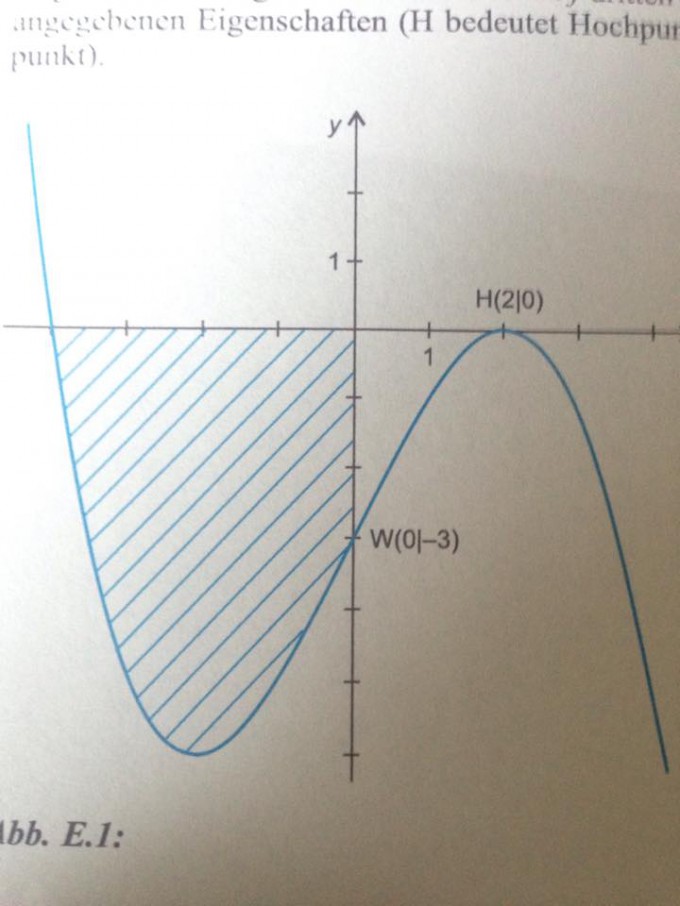
Geg: eine ganzrationale Funktion f dritten Grades mit den in der Abbildung angezeigten Eigenschaften

a)Wie lautet der Funktionsterm der Funktion f?

b) Im schraffierten Bereich von der Abbildung wird ein Dreieck so einbeschrieben, dass eine Stelle der Gleichung y= -3 hat, die zweite Seite parallel zur y-Achse verläuft und die dritte Seite den Schnittpunkt der zweiten Seite mit dem Graphen und den Wendepunkt miteinander verbindet.

Mit welchem x-Wert müsste die zweite Dreiecksseite liegen, wenn der Flächeninhalt des Dreiecks maximal werden soll?

Danke Lg 

Answer 1

Eigenschaften :
f(2) =0

f'(2) =0

f(0) = -3

f''(0 ) = 0

Eine Funktion 3ten Grades hat die Form :
ax^3+bx^2+cx+d

Setze das in die Eigenschaften ein:

Für die 1.

f(2) = 0

a2^3+b2^2+c2+d = 0

Mach das für die anderen genau so und löse dann dein Gleichungssystem.

Dann erhältst du deinen Graphen.

Und zu b :

zeichne dir doch mal das Dreieck ein und für mögliche zweite Seiten.

y= -3 bleibt ja immer gleich und die 3. hängt von der zweiten ab.

Was fällt dir auf?

Comments

Danke aber ich verstehe bei der a) leider nicht wie ich weiter machen muss, wegen den Ableitungen.. ?

Lg

---

Ganz normal Ableiten als wären a ,b,c und d Paramater:
f'(x) =3ax^2+bx+c

f''(x) = 6ax+b

---

Okay aber wie bekomme ich dann mein Glechungssystem?