Berechnen Sie, wie weit das Boot nach 120 s gefahren ist. (Integralrechnung)

Question

Aufgabe:

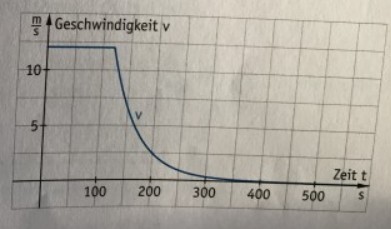
Ein Motorboot fährt zwei Minuten lang mit einer Geschwindigkeit von \( 12 \frac{\mathrm{m}}{\mathrm{s}} \). Dann wird der Motor ausgestellt und das Boot fährt noch eine Weile ohne Antrieb weiter. Die Geschwindigkeit \( v(t) \) des Bootes (in \( \frac{\mathrm{m}}{\mathrm{s}} \) ) in Abhängigkeit von der Zeit \( \mathrm{t} \) (in s) ist unten rechts als Graph dargestellt.

a) Berechnen Sie, wie weit das Boot nach \( 120 \mathrm{~s} \) gefahren ist. Wie kann man das Ergebnis im nebenstehenden Koordinatensystem veranschaulichen?

b) Erläutern Sie, wie man die Länge des bis zum Zeitpunkt t zurückgelegten Weges mithilfe von \( v(\mathrm{t}) \) berechnen kann.

c) Berechnen Sie, nach welcher Fahrstrecke das Boot praktisch zum Stillstand kommt, falls für \( t \geq 120 \) gilt: \( v(t)=132,278 \cdot 0,9802^{t} \)

d) Geben Sie allgemein an, wie man für einen mit der Geschwindigkeit \( v(t) \) bewegten Körper die Länge des im Zeitintervall \( \left[\mathrm{t}_{1} ; \mathrm{t}_{2}\right] \) zurückgelegten Weges berechnen kann.

Answer 1

Hallo Alex, gehen wir einmal Schritt für Schritt vor.

a.)
v = 12 m / s
t = 120 s
s = v * t
s = 12 m/s * 120 s
s = 1440 m

Das Produkt aus v * t entspricht in der Grafik
der Rechteckfläche v * t. Dem Rechteck mit den
Seiten x von 0 bis120 und y von 0 bis 12.
Du kannst das Rechteck einmal einzeichnen und
schraffieren. Damit ist das Ergebnis veranschaulicht.

Integralrechung entspricht im geometrischen der
Flächenberechung unter einer Funktionskurve.
Das haben wir bis 120 sec nun durchgeführt.

Der Bezug ist bei den anderen Teilfragen wird noch kommen.
Soweit verstanden ?

Comments

b.)
Die Länge der Strecke entspricht von der Zahl
dem Flächeninhalt unter der Kurve.

---

Also s setzt sich  aus der Geschwindigkeit und der Zeit zusammen.

Die  Grafik die rechts abgebildet ist, unter dem Grafen die Fläche wurde ausgerechnet oder?

---

für t <= 120 gilt
s = v * t

dann
v ( t ) = 132.278 * 0.9802^t
und der Weg
∫ v ( t ) dt =
∫ 132.278 * 0.9802^t dt
132.278 * ∫ 0.9802^t dt

Kannst du ja einmal die Stammfunktion bilden

Für eine konkrete Strecke ab t = 120 gilt
132.278 * ∫₁₂₀ ^x 0.9802^t dt

Für den Stillstand gilt
v ( t ) = 0
132.278 * 0.9802^t = 0
dürfte aber schwierig werden da die Funktion nie 0 wird

Besser
v ( t ) = 1 ( oder 0.1 )