Aufgabe Funktionenschar von ganzrationalen Funktionen:
Mithilfe eines CAS wurden drei Graphen einer ganzrationalen Funktionenschar \( \mathrm{f}_{\mathrm{k}} \) und die Gerade mit der Gleichung \( y=x \) gezeichnet. Die Abbildung gibt den wesentlichen Verlauf dieser drei Graphen wieder, das heißt in der Abbildung sind alle Nullstellen, Extremstellen und Wendestellen dieser drei Funktionen sichtbar.
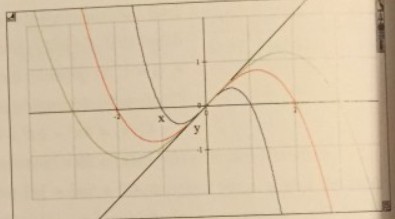
a) Welche Eigenschaften der Funktionen \( f_{k} \) lassen sich aus der Abbildung ablesen?
b) Bei der Funktion \( f_{k} \) handelt es sich um eine Funktion dritten Grades. Zeigen Sie, dass man aufgrund der Eigenschaften aus Teilaufgabe a) den Funktionsterm \( f_{k}(x)=-\frac{1}{k^{2}} x^{3}+x \) für \( f_{k} \) erhält.
c) Auf welcher Ortslinie liegen die Extrempunkte der Funktionenschar \( f_{k} \) ?
d) Begründen Sie, dass die Gerade zu \( y=x \) nicht zur Funktionenschar \( f_{k} \) gehört, jedoch als Grenzfall der Schar aufgefasst werden kann.
e) Der Flächeninhalt \( A_{k} \) der vom Graphen von \( f_{k} \) und der \( x \)-Achse eingeschlossenen Fläche verändert sich mit wechselndem k. Ermitteln Sie den funktionalen Zusammenhang zwischen \( \mathrm{k} \) und \( \mathrm{A}_{\mathrm{k}} \) in Form eines Funktionsterms.