Also: Wenn in deinem Schrägbild alle mit a beschrifteten Linien gleich lang sind, dann sollte das gestrichelte Netz symmetrisch sein. Daher sind die unteren beiden roten Winkel 30°. Der obere rote Winkel 180° - 30° - 30° = 120°.
Wenn deine mit a beschrifteten Seiten auf dem Blatt nicht gleich lang sind, ist das schwieriger zu berechnen.
Betrachte im Link oben das Tetraeder, das sich dreht. Da kommen viele Winkel vor.
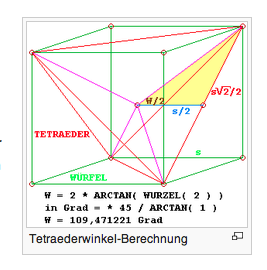
Ein gutes Schrägbild eines Tetraeder erhältst du konstruktiv, wenn du es in einen Würfel hängst, wie hier:
https://de.wikipedia.org/wiki/Tetraeder