Aufgabe:
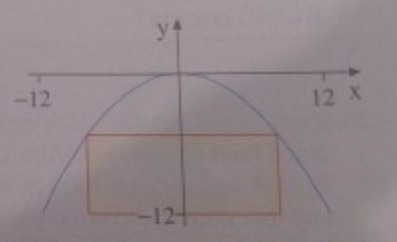
Eine 12 m hohe Tennishalle hat ein parabelförmiges Profil. In die Giebelwand soll auf der Ruckseite ein rechteckiges Kunststofffenster maximaler Fläche eingebaut werden (Abb.). Bezogen auf das eingezeichnete Koordinatensystem kann die Innenwand der Halle durch die Funktion \( y=-\frac{1}{12} x^{2} \) beschrieben werden. Die Mauer zwischen dem Fenster und der Innenwand wird modellhaft vernachlässigt. Welche Maße hat das Fenster?
Ansatz/Problem:
HB: A=a*b
NB: a = 12-1/12x² ; b = 2x
A = (12-1/12x²) 2x
A = 24x - 1/6x³
A'(x) = 24 - 0,5x²
0 = 24 - 0,5x²
x1 = 4√3
x2 = - 4√3 (entfällt)
Das Fenster hätte somit eine Länge von 13,68m und eine Breite von 11m.
Korrekt?