Ich bin Schülerin der zehnten Klasse und Mathematik ist mein größtes Hobby. Ich entschuldige eventuelle Flüchtigkeitsfehler, ich habe mir das, was hier niedergeschrieben steht, innerhalb eines Tages angeeignet und da bleiben Fehler nun mal nicht aus...trotzdem hoffe ich doch, dass dieser Tipp für einige Leute hier hilfreich ist.
a) Vektorrechnung - Basics
Bei der Vektorrechnung befinden wir uns nicht mehr im Zweidimensionalen, sondern arbeiten mit dem kartesischen Koordinatensystem. Das sieht ungefähr so aus:
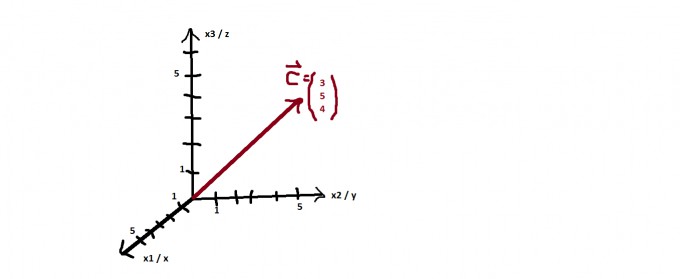
Ist jetzt nicht das Schönste, aber ich habe mir Mühe gegeben
Zu erkennen sind dort drei Achsen. Bei der Bezeichnung macht es jeder anders - die einen beschriften sie mit x1-x3, andere mit x bis z. Wichtig ist aber, dass, falls man das auf ein Karopapier überträgt, die x1-Achse so zur y-Achse steht:
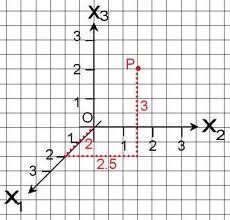
Hier seht ihr auch schon, wie man den Punkt P einträgt. In meiner etwas missglückten Zeichnung oben habe ich da so einen seltsamen Pfeil gezeichnet. Der Punkt O ist der Ursprung O(0|0|0). Wenn man hier jetzt einen Pfeil von O nach P zeichnen würde, dann würde man den Ortsvektor des Punktes P erhalten.
Dabei sieht man auch gleich einen Unterschied: Die Koordinaten eines Punktes schreibt man nebeneinander, die Koordinaten eines Vektors untereinander. Bei Vektoren sollte man wissen: Diese Vektoren gibt es unendlich viele Male genau so im Koordinatensystem. Wenn man sich meinen Vektor c nimmt und diesen irgendwo anders hin verschiebt, so bleiben seine Koordinaten gleich!
Um die Länge eines Vektors zu bestimmen, nehmt ihr einfach die Wurzel aus der Summe der Koordinaten:
$$|v| = \sqrt { x²+y²+z² } $$
Um einen Vektor von Punkt a nach b zu bestimmen, müsst ihr einfach den "Satz" hinten minus vorn im Kopf haben - das heißt, man nimmt die Koordinaten des Zielpunktes und subtrahiert die Koordinaten des Startpunktes.
b) Das Skalarprodukt und das Kreuzprodukt
Das Skalarprodukt ist einfach eine reelle Zahl. Mit dem Skalarprodukt kann man zum Beispiel den Schnittwinkel zwischen zwei Vektoren berechnen. Das Skalarprodukt sieht wie folgt aus:
$$ \vec{ a }* \vec{ b } = |\vec{ a }|*|\vec{ b }|*cos φ $$
wobei φ der Schnittwinkel zweier Vektoren ist.
Ist das Skalarprodukt null, so stehen die Vektoren senkrecht aufeinander.
Kommen wir nun zum Kreuzprodukt. Mit diesem kannst du dir den Normalenvektor ausrechnen, wenn du beispielsweise eine Ebene hast und diese in die Koordinatenform umformen willst (dazu im Kapitel "Ebenen" mehr). Beim Kreuzprodukt erhält man einen Vektor, der zu den beiden orthogonal ist.
Die Rechnung sieht etwa wie folgt aus:
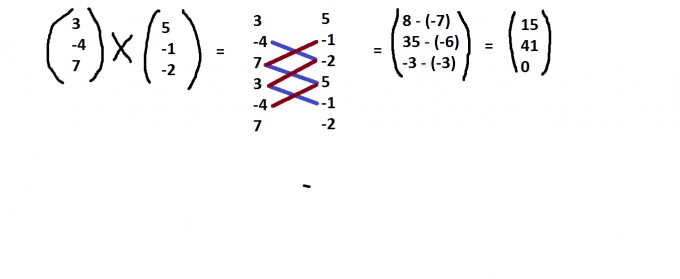
Als nächste folgen c (Ebenen) und d (Geraden), siehe Vektoren Teil 2.