Im zweiten Tipp geht es weiter mit dem Ziehen mit einem Griff, nachdem ich im ersten Teil das mehrmalige Ziehen vorgestellt habe.
Wir stellen uns eine Urne vor, die fünf rote und drei blaue Kugeln enthält:

Die Grafik ist jetzt kein Meisterwerk, sie soll nur der Anschaulichkeit dienen.
Nun muss man sich überlegen:
Wie viele Möglichkeiten habe ich eigentlich, diese ganzen Kugeln anzuordnen?
Eine Möglichkeit ist diese hier:

Es gibt doch aber noch viel mehr Möglichkeiten diese acht Kugeln anzuordnen, nämlich 8! Möglichkeiten. Man sagt "8 Fakultät".
Lasst euch von diesem Ausrufezeichen bei der Acht nicht verwirren, dies ist hier das mathematische Zeichen für die Fakultät. Diese ist sehr wichtig.
Man stelle sich das so vor: Man hat diese acht Kugeln und acht Plätze. Es gibt acht Möglichkeiten für die erste Kugel. Für die zweite Kugel gibt es noch sieben Möglichkeiten usw., sodass es für die letzte Kugel noch genau einen freien Platz gibt. Ausgeschrieben ist die Fakultät also:
8! = 8*7*6*5*4*3*2*1 = 40.320 Möglichkeiten (wenn man missachtet, dass diese Kugeln eine Farbe haben).
Nun sagen wir zunächst, wir wollen die Möglichkeiten bestimmen, die blauen Kugeln zu platzieren, wenn die roten schon platziert sind. Das sind logischerweise 3! Möglichkeiten. Wir können das jetzt auch umdrehen und sagen, die blauen seien platziert und die roten sollen noch platziert werden, dann gibt es für die roten Kugeln noch 5! Möglichkeiten.
Da die Kugeln ja unterschiedliche Farben haben, gibt es insgesamt folgende Möglichkeiten, die Kugeln anzuordnen:
$$ \begin{pmatrix} 8\\3\\ \end{pmatrix} = \begin{pmatrix} 8\\5\\ \end{pmatrix} = 56$$
Dies spricht man "Acht über 3 / 5 bzw. 3 / 5 aus 8".
Und warum ist 8 über 3 das gleiche wie 8 über 5?
Hier kommen wir zu der Formel, den Binomialkoeffizienten. Der Binomialkoeffizient lautet wie folgt:
$$ \begin{pmatrix} n\\k\\ \end{pmatrix} = \frac { n! }{ k!\cdot(n-k)! } $$
Hiermit kann man nun obriges erklären. Hier ist ja einmal n=8 und k=3 sowie n=8 und k=5. Stellen wir nun für beide Fälle den Binomialkoeffizienten auf:
$$ \begin{pmatrix} 8\\5\\ \end{pmatrix} = \frac { 8! }{ 5!\cdot(8-5)! } = \frac { 8! }{ 5!\cdot3! }$$
$$ \begin{pmatrix} 8\\3\\ \end{pmatrix} = \frac { 8! }{ 3!\cdot(8-3)! } = \frac { 8! }{ 5!\cdot3! }$$
=> Das ist das gleiche!
Mit dem Binomialkoeffizienten lässt sich also die Anzahl der Möglichkeiten bestimmen. Dass 8 über 5 das gleiche wie 8 über 3 ist, kann man sich auch gut am Pascalschen Dreieck klar machen (und dann wisst ihr auch, woher der Name kommt):

Hier sehr ihr, wie zunächst die binomischen Formeln (3. Zeile) und das Pascalsche Dreieck zusammen hängen. Dort wird jeweils der Exponent um Eins erhöht und in der entsprechenden Zeile sieht man dann das Ergebnis.
Und was hat das jetzt mit dem Binomialkoeffizienten zu tun?
Man betrachte auch folgende Abbildung:
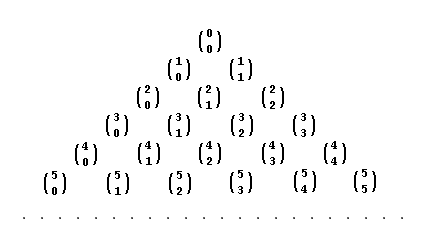
Das ist auch das Pascalsche Dreieck, bloß mit den Binomialkoeffizienten dargestellt. Schaut man in die Zeile, so erhält man das n. Schaut man in die "Spalten" bzw. Plätze in der jeweiligen Zeile, so sieht man, dass k immer von links nach rechts um eines größer wird.
Da sollten einem auch drei Dinge auffallen:
$$ k = n: \begin{pmatrix} n\\k\\ \end{pmatrix} = 1$$
$$ k = 1: \begin{pmatrix} n\\k\\ \end{pmatrix} = n$$
$$ k = 0: \begin{pmatrix} n\\k\\ \end{pmatrix} = 1$$
Im nächsten Tipp fahre ich dann mit der Bernoulli-Kette fort.