1. Einleitung
Wer hätte gedacht, dass der beliebte Videospiel-Klassiker „Banjo und Kazooie“ aus dem Entwicklerhaus Rare fast 19 Jahre nach seinem Erscheinen zum „Mathe machen“ motivieren würde? [1] Ich als damals 5-Jähriger konnte das natürlich nicht ahnen. Und nun sitze ich hier und schreibe diesen Artikel, um zu zeigen, wie auch das populäre Unterhaltungsmedium „Videospiele“ didaktisch wertvoll zum Einsatz kommen kann.
2. Das Problem
Ziel des Spiels ist das Einsammeln von Jiggies, die man als Belohnung für das Lösen unterschiedlicher Aufgaben erhält. In diesem Fall musste das Pyramiden-Memory innerhalb des vorgegebenen Zeitlimits gelöst werden. Da die Bildpositionen in allen Spielkopien und Speicherständen gleich sind, kann man dieses Rätsel durch simples Auswendiglernen der Lösung ohne einen einzigen Fehler schaffen. Wie verhält es sich aber, wenn der Spieler die Positionen nicht kennt?
Wie hoch ist die Wahrscheinlichkeit, dass er in diesem Fall ohne einen Fehler Erfolg haben wird?
3. Die Lösung
Sei X die Anzahl der Fehler, die im Spielverlauf vor erfolgreichem Beenden des Memorys gemacht werden. Die Bildpositionen sind zudem nicht bekannt. Wir suchen also: $$P(X=0)$$ Fassen wir die für unsere Berechnungen relevanten Parameter in einem kurzen Datenblatt zusammen:
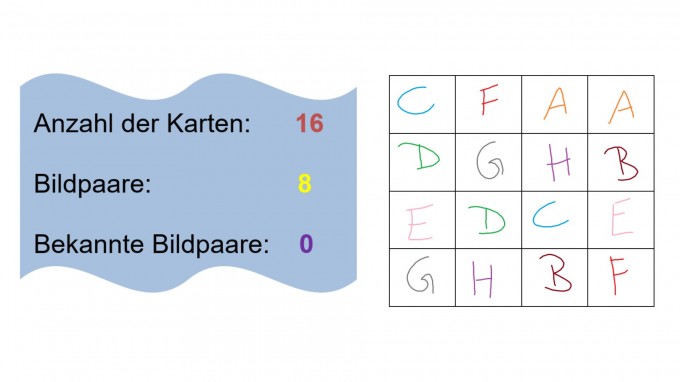
Am Anfang ist es unerheblich, welche Karte wir aufdecken, weil noch kein Fehler gemacht werden kann. Da jedoch danach eine konkrete Karte aufgedeckt wird, muss das dazu passende Gegenstück unter den verbliebenen 16-1 = 15 Karten zufällig gefunden werden. Die Wahrscheinlichkeit dafür beträgt $$\dfrac{1}{15}$$ Jetzt befinden wir uns wieder in der Situation, dass eine ausgewählte Karte noch zu keinem Fehler führen kann, denn schließlich ist die Reihenfolge, in der die Bildpaare aufgedeckt werden, nicht relevant. Im nächsten Schritt ist dann allerdings erneut aus den verbliebenen 16-1-1-1=13 Karten das zum zuvor aufgedeckten Bild passende Pendant zu finden. Die Wahrscheinlichkeit eines Erfolges ist dabei $$\dfrac{1}{13}$$ Dieser Gedankengang wird so lange fortgesetzt, bis keine Karten mehr aufzudecken sind. $$ \underbrace{\dfrac{16}{16}}_{=1}\cdot\dfrac{1}{15}\cdot \underbrace{\dfrac{14}{14}}_{=1}\cdot\dfrac{1}{13}\cdot \underbrace{\dfrac{12}{12}}_{=1}\cdot\dfrac{1}{11}\cdot \underbrace{\dfrac{10}{10}}_{=1}\cdot\dfrac{1}{9}\cdot \underbrace{\dfrac{8}{8}}_{=1}\cdot\dfrac{1}{7}\cdot \underbrace{\dfrac{6}{6}}_{=1}\cdot\dfrac{1}{5}\cdot \underbrace{\dfrac{4}{4}}_{=1}\cdot\dfrac{1}{3}\cdot \underbrace{\dfrac{2}{2}}_{=1}\cdot\dfrac{1}{1}=\dfrac{10321920}{16!}=\dfrac{1}{2027025} \approx 0.000049\%$$ Ich als Mathematiker habe mir direkt nach der Lösung dieses Problems die Frage gestellt, wie die Wahrscheinlichkeit wohl für insgesamt $$n\text{ Karten mit }\dfrac{n}{2}\text{ Bildpaaren}$$ aussieht. Wenn wir den vorherigen Gedankengang adaptieren, erhalten wir folgende Formel: $$\dfrac{n}{n}\cdot\dfrac{1}{n-1}\cdot\dfrac{n-2}{n-2}\cdot \dfrac{1}{n-3}\cdot \cdot \dfrac{4}{4}\cdot\dfrac{1}{3}\cdot\dfrac{2}{2}\cdot\dfrac{1}{1}=\dfrac{1}{n!}\cdot \prod_{k=1}^{0.5n}{2k}$$
Ich hoffe, dass euch mein erster Mathe-Artikel gefallen hat und freue mich auf euer Feedback!
André
Quellenverzeichnis:
[1] https://www.gamerpedia.de/Banjo-Kazooie (29.01.2017)
Das Mitglied hat durch den Artikel 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.