Mathe-Artikel: LR Zerlegung - Zeilen-Spalten-Pivot - Gaußelimination zur Lösung eines R^4 LGS

Question

Sei A = [a_ij] ∈ R^4x4    und P^ij , Q^ij Elementarmatrizen zum Zeilentausch i<->j / Spaltentausch i<->j

\(\small A :=\left[\begin{array}{cccc}2 & 1 & -3 & 4 \\ 4 & 1 & -4 & 9 \\ -2 & 1 & 0 & -5 \\ 2 & 2 & -5 & 1\end{array}\right] \)

a₂₄ = 9 Pivot (Betragsgrößtes Element) für Zeilen/Spaltentausch

A:= P₁²¹ A Q₁¹⁴

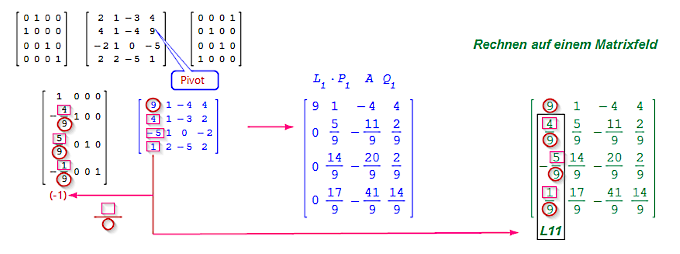
Die Faktoren der Gaußelimination in Matrix L₁ bilde ich aus dem Pivot a₁₁ = 9 als Nenner und den Spaltenelementen a_j1 =[4,-5,1] als Zähler multipliziert mit (-1) ==> (-1) [ 4/9,-5/9,1/9 ] ==> 1.Spalte nach l₁₁ in L₁ ==> L₁ A ergibt Nullen in der 1. Spalte a_j1 j=2..n. In die mit Nullen belegten Matrixelemente L11 schreibe ich die Faktoren der Gaußelimination, ohne Multiplikation (-1).

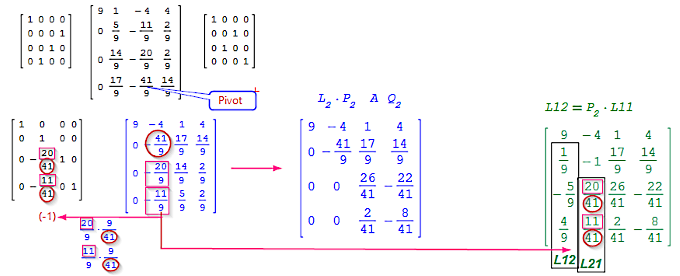
Pivot a₄₃ =-41/9 ===> a₂₂=-41/9:
P₂⁴² A Q₂²³
Bildung der Gaußeleminationsfaktoren Zähler a_2j (-1) [-20/9, -11/9], Nenner a₂₂=-41/9 ==> 2. Spalte nach a₂₂ in L₂ = (-1) [ -20/9, -11/9 ](-9/41). L₂ A ergibt Nullen in 2. Spalte von A . In die mit Nullen belegten Elemente des Matrixfeldes L21 schreibe ich die Faktoren der Gaußelimination, ohne Multiplikation (-1). In Spalte L12 übertrage ich den Zeilentausch P₂ L11 aus diesem Schritt.

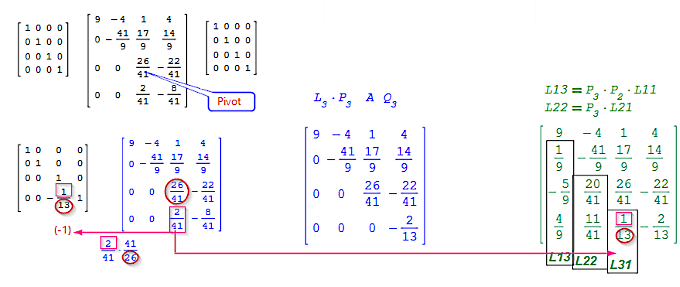
Im 3. Schritt sind keine Zeilen/Spaltentausche notwendig - P₃, Q₃ = Identity(n).
Pivot a₃₃=26/41 wird Nenner und a₄₃=2/41 wird Zähler des Gaußeleminationsfaktors in L₃ multipliziert mit (-1) l₄₃=-1/13 macht in a₄₃ eine Null und wird als L31 in die freiwerdende Stelle des Matrixfeldes geschrieben. Im allgemeinen Fall müssen die Zeilentausche dieses Schrittes, P₃*L12=>L13 und P₃*L21 => L22, nachgeführt werden.

LR in einem Matrixfeld

\( \left[\begin{array}{cccc}9 & -4 & 1 & 4 \\ \textcolor{red}{ \frac{1}{9} }& \frac{-41}{9} & \frac{17}{9} & \frac{14}{9} \\ \textcolor{red}{-\frac{5}{9}} & \textcolor{red}{\frac{20}{41}} & \frac{26}{41} & -\frac{22}{41} \\ \textcolor{red}{\frac{4}{9}} & \textcolor{red}{ \frac{11}{41} }& \textcolor{red}{\frac{1}{13}} & -\frac{2}{13} \\ \textcolor{red}{ L_{13}}&\textcolor{red}{ L_{22}} &\textcolor{red}{ L_{31}} & \end{array}\right] \)

Die vielleicht übersichtlichste Methode, wenn man die Buchführung in den Griff bekommt.

Beispielapp dazu: https://www.geogebra.org/m/c94bmjuy

Zusammenfassung

\(\small P:=P_{3} \cdot P_{2} \cdot P_{1}=\left[\begin{array}{llll}0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0\end{array}\right] \)

\(\small Q:=Q_{1} \cdot Q_{2} \cdot Q_{3}=\left[\begin{array}{llll}0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\end{array}\right] \)

\(\small L:=\left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ \frac{1}{9} & 1 & 0 & 0 \\ -\frac{5}{9} & \frac{20}{41} & 1 & 0 \\ \frac{4}{9} & \frac{11}{41} & \frac{1}{13} & 1\end{array}\right] \)

\(\small R=\left[\begin{array}{cccc}9 & -4 & 1 & 4 \\ 0 & -\frac{41}{9} & \frac{17}{9} & \frac{14}{9} \\ 0 & 0 & \frac{26}{41} & -\frac{22}{41} \\ 0 & 0 & 0 & -\frac{2}{13}\end{array}\right] \)

Lösung LGS

\(P \cdot A \cdot Q=L \cdot R, \\ A \cdot X=b,\\ A \cdot Q \cdot Q^{T} \cdot X=b, \\ P \cdot A \cdot Q \cdot Q^{T} \cdot X=P \cdot b, \\ L \cdot R \cdot Q^{T} \cdot X=P \cdot b\)

\( R \cdot\left(Q^{T} \cdot X\right)=Y \)

\( L \cdot Y=P \cdot b \quad===>\quad \quad==\Rightarrow \quad Y \quad \) Vorwärts-Einsetzen

\( \left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ \frac{1}{9} & 1 & 0 & 0 \\ -\frac{5}{9} & \frac{20}{41} & 1 & 0 \\ \frac{4}{9} & \frac{11}{41} & \frac{1}{13} & 1\end{array}\right]\left[\begin{array}{l}y_1 \\ y_{2} \\ y_{3} \\ y_{4}\end{array}\right]=\left[\begin{array}{llll}0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0\end{array}\right]\left[\begin{array}{c}1 \\ 4 \\ 6 \\ -1\end{array}\right] \to \left[\begin{array}{c} 4 \\  -\frac{13}{9} \\  \frac{366}{41} \\  -\frac{14}{13}\end{array}\right] \)

\( R \quad Q^{T} \cdot X=Y \quad ===>\quad Q^{\mathrm{T}} \cdot X \quad \) Rückwärts-Einsetzen

\( \left[\begin{array}{cccc}9 & -4 & 1 & 4 \\ 0 & -\frac{41}{9} & \frac{17}{9} & \frac{14}{9} \\ 0 & 0 & \frac{26}{41} & -\frac{22}{41} \\ 0 & 0 & 0 & -\frac{2}{13}\end{array}\right]\left[\begin{array}{c}x_4 \\ x_3 \\ x_2 \\ x_1\end{array}\right]=\left[\begin{array}{c}4 \\ -\frac{13}{9} \\  \frac{366}{41} \\  -\frac{14}{13}\end{array}\right] \to \left[\begin{array}{c}7 \\ 20 \\ 11 \\ 0\end{array}\right]\)

\( \left[\begin{array}{cccc}2 & 1 & -3 & 4 \\ 4 & 1 & -4 & 9 \\ -2 & 1 & 0 & -5 \\ 2 & 2 & -5 & 1\end{array}\right] \quad\left[\begin{array}{c}7 \\ 20 \\ 11 \\ 0\end{array}\right]=\left[\begin{array}{c}1 \\ 4 \\ 6 \\ -1\end{array}\right] \)

Live-Arbeitsblatt SMath (MathCad-Clone)→

Spaltenpivotsuche - in jeden Schritt die Spaltentausch-Matrizen durch eine Einheitsmatrix ersetzen

Q_step:=T(step,q,n) ==> Q_step:=T(step,step,n) ==> ändern

Für R³ anpassen - step::=3 ändern und b Vektor kürzen

L_step:=identity(n), b:=mat(b₁,b₂,b₃,3)