Koordinaten des Scheitels in Abhängigkeit von k berechnen: y= 2x²+kx-(k²/2)+2,5

Question

2x²+kx-(k²/2)+2,5 Kann mir jemand helfen diese Aufgabe zu lösen? Wir schreiben morgen Schulaufgabe :)

Comments

Ist das eine andere Funktionenschar wie vorher?

Oder soll es hier 2x²+kx-(k²/2)x+2,5 heissen?

---

Das stimmt schon so :)

Answer 1

über hundert erklärte Beispiele:

https://www.mathelounge.de/tag/scheitelpunktform

und da Erklärungen:

https://de.search.yahoo.com/search?p=scheitelpunktform&ei=UTF-8&fr=moz35

Comments

Ich kanns ja, aber diese Aufgabe ist "anders"

---

was ist da anders ?

Umformen zur Scheitelpunktform . Ob da k oder kakwadraht oder Pferdeäpfel stehen - die Formel ist immer die gleiche.

Answer 2

Falls du Differtialrechnung schon kannst.

f ( x ) = 2x²+kx-(k²/2)+2,5
f ´( x ) = 4x + k

4x + k = 0
4x = -k
x = -k/4

Den Funktionswert berechnen
f ( -k/4) = 2 * ( -k/4)^2 + k * ( -k/4) - ( k^2 / 2) + 2.5
f ( -k/4) = 2 * ( -k^2/16 ) - k^2 / 4 -  k^2 / 2 + 2.5
f ( -k/4) =  k^2/ 8 - 2 * k^2 / 8 - 4 * k^2 / 8 + 2.5
f ( -k/4) =  -5 * k^2/ 8 + 2.5

S ( - k / 4  | ( -5 / 8 ) * k^2 + 2.5 )

Answer 3

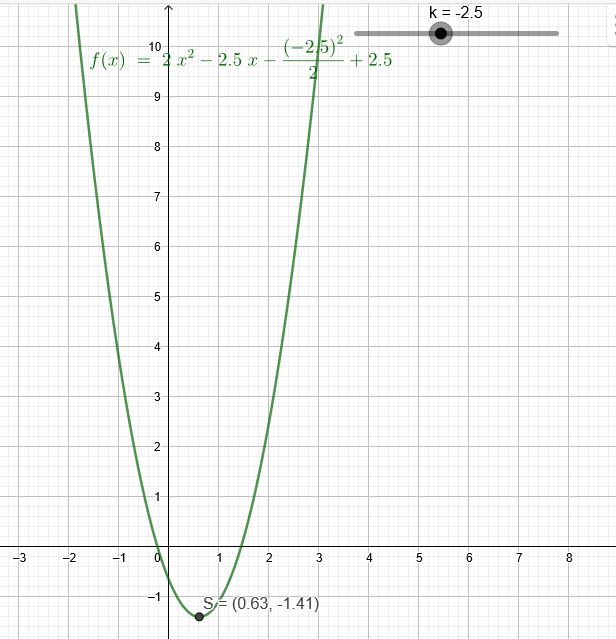
Koordinaten des Scheitels in Abhängigkeit von \(k\) berechnen:

\(y= 2x^2+k*x- \frac{k^2}{2} +2,5   |:2 \)

\(\frac{y}{2}= x^2+\frac{k}{2}*x- \frac{k^2}{4} +\frac{5}{4}      |+\frac{k^2}{4}-\frac{5}{4}  \)

\(\frac{y}{2}+\frac{k^2}{4}-\frac{5}{4} = x^2+\frac{k}{2}*x  \)

\(\frac{y}{2}+\frac{k^2}{4}-\frac{5}{4}+(\frac{k}{4})^2 = (x+\frac{k}{4})^2  \)

\(\frac{y}{2}+\frac{4k^2}{16}-\frac{5}{4}+\frac{k^2}{16} = (x+\frac{k}{4})^2  \)

\(\frac{y}{2}+\frac{5k^2}{16}-\frac{5}{4} = (x+\frac{k}{4})^2      |*2  \)

\(y+\frac{5k^2}{8}-\frac{5}{2} = 2*(x+\frac{k}{4})^2      |+\frac{5}{2} -\frac{5k^2}{8} \)

\(y = 2*(x+\frac{k}{4})^2+\frac{5}{2}-\frac{5k^2}{8} \)

\(S(-\frac{k}{4}|\frac{5}{2}-\frac{5k^2}{8})\)