Hallo :)
a) Es sind die Ergebnisse möglich:
(R|1); (R|2); (R|3); (B|1); (B|2); (B|3)
=> Am besten machst du dir das am unten stehenden Baum klar.
Die Räder werden zwar gleichzeitig gedreht, allerdings kannst du das auch so betrachten, als würdest du dies hintereinander ausführen. Du kannst erst die erste Scheibe drehen, bei der es zwei Möglichkeiten gibt - rot oder blau. Nun hast du noch dein zweites Rad, welches du anschließend drehst. Da hast du streng genommen sechs Möglichkeiten: 1, 2, 3, 1, 2, 3. Aber schau mal, es sind drei Mal ein "Zahlenpaar" von gleichen Zahlen auf dem zweiten Rad notiert. Also gibt es drei Möglichkeiten: 1, 2 oder 3. Deshalb hat der zweite "Zug" drei Möglichkeiten und nicht 6. Man hätte das zweite Rad auch dritteln können und dann da jeweils 1, 2 und 3 rauf schreiben können. Es ist nämlich wie bereits erwähnt. Jedes dieser Ziffern hat hier erstmal 1/6 des Rades "eingenommen". Aber du hast ja die Ziffer 1, 2 und 3 jeweils zwei Mal. Das heißt, die Wahrscheinlichkeit für eine 1 ist zum Beispiel 1/6 + 1/6 = 2/6 = 1/3. Das gilt auch für 2 und 3.
b) Du rechnest die Wahrscheinlichkeiten aus. Dein Baum sieht dann so aus:
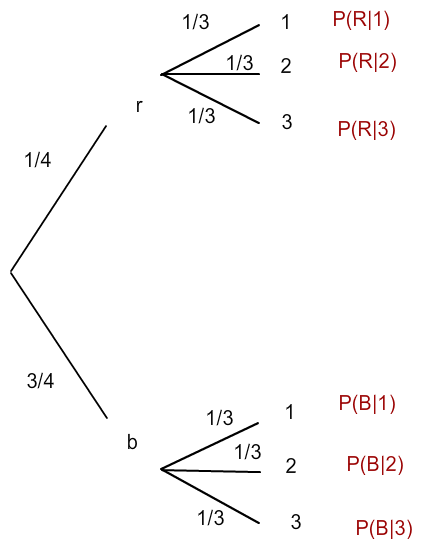
Nun Bestimmst du nach der Pfadmultiplikationsregel deine Wahrscheinlichkeiten:
P(R|1) = P(r)*P(1) = 1/4 * 1/3 = 1/12
P(R|1) = P(R|2) = P(R|3) = 1/12
P(B|1) = P(B) * P(1) = 3/4 * 1/3 = 3/12
P(B|1) = P(B|2) = P(B|3) = 3/12
=> (3/12)*3 + (1/12) * 3 = 9/12 + 3/12 = 12/12 = 1
=> Die Wahrscheinlichkeiten stimmen so.
Ich hoffe, dass ich etwas Licht ins Dunkle bringen konnte :)
Bei Fragen melde dich.