Schnittpunkt der beiden Geraden graphisch ermitteln 1. 5y-2-x=0, 2. 6y-x-3=0

Question

Ermittlung des Schnittpunktes der beiden Geraden, mit Auflösung nach y, erstellen eines Graphen

1. 5y-2-x=0

2. 6y-x-3=0

Answer 1

Der Lösungsweg ist oben schon angegeben

1.  5y-2-x  =0      |+x ,+2  , /5

             y= (x+2)/5

2.  6y-x-3   =0         |  +x, +3, /6

              y= (x+3)/6

Gleichsetzen

              (x+2)/5=(x+3)/6       |   *5, *6

            6(x+2)   =5(x+3)

            6x+12    =5x+15        | -5x , -12

                       x=3

                        y=1

Der Schnittpunkt ist  S(3|1)

Answer 2

Hi,

zum Finden der Schnittpunkte würde ich nach x auflösen und gleichsetzen.

1. 5y-2-x=0
2. 6y-x-3=0

1. x=5y-2
2. x=6y-3

Gleichsetzen:

5y-2=6y-3    |-5y+3
y=1

Demnach x=3 (in Gleichung 1 oder 2 einsetzen).

Und S(3|1).

 

Da Du noch zeichnen willst, musst Du aber noch nach y umformen. Die Gerade hat ja die Form y=mx+b. Das gerade nach x aufzulösen, war nur sinnvoll, weil man sehr einfach weiterrechnen kann (ohne Brüche etc).

Also:

1. y=(x+2)/5=x/5+2/5

2. y=(x+3)/6=x/6+1/2

 

Das noch in den Graphen:

 

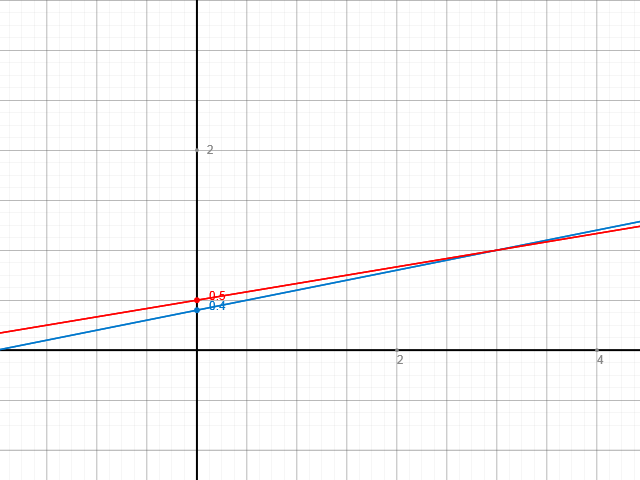
Du siehst also, es passt.

 

Grüße