Kurvendiskussion rückwärts mit Graphen von ganzrationalen Funktionen.

Question

Danke und Kussi im voraus :))

Aufgabe

Arbeitsauftrag - Aufgabenblatt "Kurvendiskussion rückwärts" weiterbearbeiten´

Lest die entsprechenden Punkte aus den untenstehenden Graphen ab und stellt eine passende Funktionsgleichung auf.

Der Graph gibt den Verlauf einer Straße an. Finde eine ganzrationale Funktion.

Tipp: Funktion 3. Grades

Tipp: Funktion 5. Grades

Achtet auch auf Punkt- oder Achsensymmetrie!

 

Answer 1

Funktion 3. Grades ist allgemein:
f(x) = ax^3+bx^2+cx+d

5. Grades:

g(x) = ax^5+bx^4+cx^3+dx^2+ex+f

Du musst jetzt Gleichungen aufstellen,mit denen du deine Parameter a,b,c..., bestimmen kannst.

Diese Gleichungen lassen sich aus den Bildern ablesen.

Z.b.
a)

f(0)= 0

0 = a0^3+b0^2+c0+d

=> d= 0

Tipp:
Für die Extremstellen gilt f'(0) = 0

Wendepunkte f''(0 ) = 0 .

Bilde die Ableitungen der allgemeinen Funktionen.

Answer 2

f ( x ) = a*x^3 + b * x^2 + c * x + d
Aus der Zeichnung
d = 0
Punktsymmetrie zum Ursprung bedeutet
f ( x ) = a*x^3 + c * x
f ( 1 ) = a + c = -2
f ´( x ) = 3 * a * x^2 + c
f ´( 1 ) = 3 * a * 1 + c = 0  ( Extrempunkt )
3a + c = 0
a + c = -2
--------------
2a = 0 - ( -2)
2a = 2
a = 1
a + c = -2
1 + c = -2
c = -3

f ( x ) = x^3 - 3 * x

f (1 ) 1 - 3 = -2  | stimmt
f ´( 1 ) = 3 * 1^2 - 3 = 0  | stimmt auch

Alle Angaben ohne Gewähr.

Comments

b.)
Es entfallen die Glieder mit geradem Exponenten
und der y-Achsenabschnitt
f ( x ) = a * x^5 + b * x^3 + c * x
f ´( x ) = 5a * x^4 + 3b * x^2 + c

f ( 1 ) = 2
f ´( 1 ) = 0  ( Extrempunkt )
f ( -1 ) = -2

Vielleicht reicht dir das zur Lösung schon.

---

ich weiß die Frage gehört nicht hierhin, aber Können Sie mir bitte bitte helfen?

https://www.mathelounge.de/206306/ableitung-hilfe-losungen-vorhanden

Ich möchte es gerne verstehen.

Grüße

Answer 3

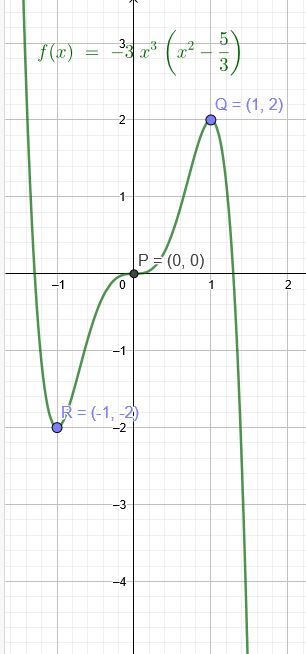
b) Sattelpunkt bei P(0|0)     Maximum bei Q(1|2)   Minimum bei R(-1|-2)

\(f(x)=a*x^3*(x-N_1)*(x-N_2) \)  Da die Nullstellen spiegelbildlich zum Sattelpunkt sind , gilt:

\(f(x)=a*x^3*(x-N)*(x+N)= a*x^3*(x^2-N^2)\)

\(Q(1|2)\)

\(f(1)= a*(1-N^2)=2\) → \( a=\frac{2}{1-N^2}\)

\(f(x)=\frac{2}{1-N^2}*[x^5-x^3*N^2]\)

\(f´(x)=\frac{2}{1-N^2}*[5x^4-3x^2*N^2]\)

\(f´(1)=\frac{2}{1-N^2}*[5-3*N^2]=0\)     \(N^2=\frac{5}{3}\)      \( a=\frac{2}{1-\frac{5}{3}}=-3\)

\(f(x)= -3*x^3*(x^2-\frac{5}{3})\)