Wie berechne ich die Nullstellen: ft(x) = 1/3x^2+tx-2/3x-t

Question

, wie berechne ich die nullstellen bei dieser aufgabe ft(x)= 1/3x²+tx-2/3x-t

ich hoffe ihr könnt mir helfen

Comments

Steht jeweils nur die 3 unter dem Bruchstrich?

Dann ist  das 1/3x²+tx-2/3x-t = 1/3x²+(t-2/3) x-t = 0 eine quadratische Gleichung.

Nimm die Formel für quadratische Gleichungen.

Answer 1

Da du hier Polynome zweiten Grades hast einfach mit der Mitternachtsformel.

$$a=\frac { 1 }{ 3 } \\ b=(t-\frac { 2 }{ 3 } )\\ c=-t$$

Diese Werte setzt jetzt einfach ein und vereinfachst so weit wie möglich. Die beiden Ergebnisse sind deine Nullstellen ;)

Gruß

EmNero

Comments

habe vorher noch nie mit der mitternachtsformel gerechnet. wie rechne ich den ab hier weiter? :D

---

Ich reche dir mal die Diskriminante vor:

b²-4ac

(t-(2/3))²-4*(1/3)*(-t)

t²-(4/3)t+4/3 +4/3t

t²+4/3

---

Simon kannst Du mir mal auf fb antworten?^^ es geht um Wirtschaft :D

---

Ja^^ ........

Answer 2

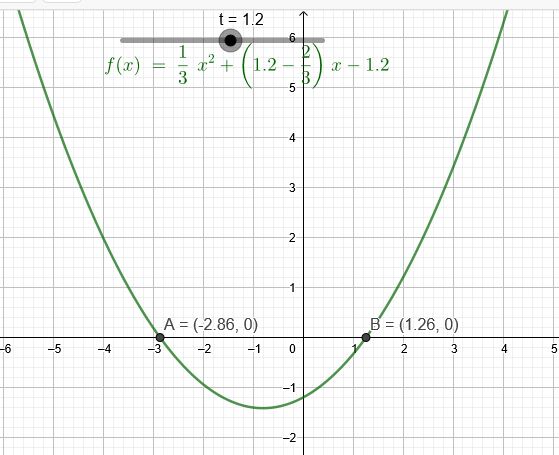
\(\frac{1}{3}*x^2+(t-\frac{2}{3}) *x-t = 0\)

\(x^2+(3*t-2) *x = 3t\)

\((x+(1,5t-1))^2 = 3t+(1,5t-1)^2\)

\((x+(1,5t-1))^2 = 3t+2,25t^2-3t+1\)

\((x+(1,5t-1))^2 =2,25t^2+1  |  \sqrt{~~}\)

1.)

\(x+(1,5t-1) =  \sqrt{2,25t^2+1}\)

\(x_1 =1-1,5t +\sqrt{2,25t^2+1}\)

2.)

\(x+(1,5t-1) = - \sqrt{2,25t^2+1}\)

\(x_2 =1-1,5t -\sqrt{2,25t^2+1}\)