Aufgabe:
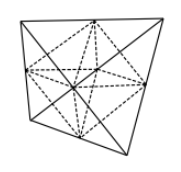
Zwei reguläre Tetraeder mit gleicher Kantenlänge durchdringen einander so, dass jede Fläche durch die Mittelpunkte von drei Kanten geht, die von einer Ecke ausgehen. Die Vereinigung \( V \) der beiden Tetraeder ist ein dreidimensionaler "Stern".
a) Sei \( D \) der Körper, der aus allen Punkten besteht, die zu beiden Tetraedern gehören. Beschreiben Sie diesen "Durchdringungskörper".
b) In welchem Verhältnis stehen die Volumen von \( V \) und \( D \)?
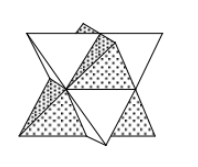
a) Der Durchdringungskörper hat 12 Kanten und 8 gleichseitige Dreiecke als Flächen. \( D \) ist ein Oktaeder.
b) Der Oktaeder \( D \) entsteht dadurch, dass von einem Tetraeder (Volumen \( T \) ) vier kleine Tetraeder mit halber Kantenlänge abgeschnitten werden.
Daher ist das Volumen jedes dieser kleineren Tetraeders \( \frac{1}{8} T \).
Also ist das Oktaedervolumen \( D=T-4 \cdot \frac{T}{8}=\frac{T}{2} \) und \( V=T+4 \cdot \frac{T}{8}=\frac{3}{2} T \)
Somit ist \( \frac{V}{D}=3 \)