Aufgabe:
Die abgebildete Vase eines finnischen Designers hat die Form eınes Kotationskörpers. Die erzeugenden Kurven sind zwei Parabelstücke, die in einem geeigneten Koordinatensystem gegeben sind durch:
\( f(x)=-0,03 x^{2}+0,6 x+5 \text { mit } x \in[0 ; 20[ \)
und
\( g(x)=0,12 x^{2}-5,4 x+65 \text { mit } x \in[20 ; 30] \)
Eine Längeneinheit entspricht \( 1 \mathrm{~cm} \).
Die Wandstärke der Vase ist vernachlässigbar.

2.1 Zeichnen Sie den Längsschnitt der Vase.
2.2 Bestimmen Sie den Radius der Vase am Boden und am oberen Rand. Bestimmen Sie den kleinsten Umfang der Vase.
2.3 Welche der folgenden drei Abbildungen könnte die Füllmenge der Vase in Abhängigkeit von ihrer Füllhöhe beschreiben? Begründen Sie Ihre Entscheidung. Was sagen die Wendestellen der Füllkurve über die Vase aus?
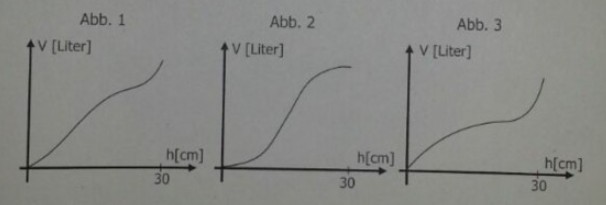
2.4 Die Vase ist \( 29 \mathrm{~cm} \) hoch mit Wasser gefullt. Nun sollen langstielige Blumen hineingestellt werden.
Wie viele Blumen mit einem Stieldurchmesser von \( 1 \mathrm{~cm} \) passen in die Vase, ohne dass das Wasser überläuft? Nehmen Sie zur Vereinfachung an, dass die Stiele zylinderförmig sind und senkrecht auf den Boden der Vase gestellt werden.
(Abitur 2008 , Baden-Württemberg)