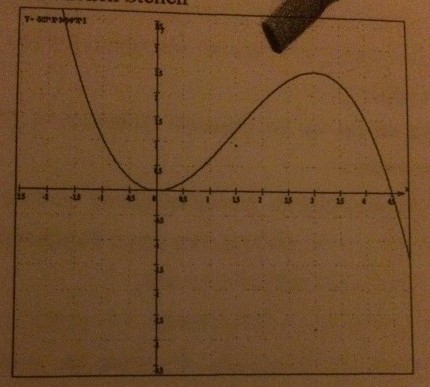
Aufgabe - Peter, der korrekte Autofahrer:
Peter rühmt sich,ein besonders korrekter Autofahrer zu sein. "Gestern",so sagt er,habe ich für die 2,5km lange Ortskurzfahrt im Marl genau 3 Minuten benötigt." War Peter so korrekt,oder hat er dabei nur Glück gehabt,dass an manchen Stellen keine geschwindigkeitskontrolle war?
Die Auswertung des elektronischen Fahrtenbuchs,das die Fahrzeit und die zurückgelegte Strecke speichert,hat ergeben,dass die weg-Zeit Funktion ungefähr durch eine Ganzrationale Funktion dritten Grades beschrieben werden kann. f(x)= - 5/27xhoch3 + 5/6x^2.
a) Wie kommt Peter zu der Aussage, dass er ein korrekter Autofahrer ist? Gibt es Zeitintervalle, in denen er schneller/langsamer als 50 km/h gefahren ist?
b) Wie müsste der Funktionsgraph aussehen, wenn Peter korrekt gefahren ist? Geben Sie auch eine Funktionsgleichung an.
c) Peter hat erfahren,dass nach 1,5 MInuten Fahrzeit die Geschwindigkeit gemessen wurde. Muss er mit einem Bußgeldbescheid rechnen?