Welche Abmessungen soll der Querschnitt haben, damit das Fassungsvermögen des Grabens maximal wird?

Question

Aufgabe:

Ein langer Graben des skizzierten Querschnittes wird durch Auskleiden mit einer Kunststoffbahn der Breite B wasserdicht gemacht. Welche Abmessungen soll der Querschnitt haben, damit das Fassungsvermögen des Grabens maximal wird?

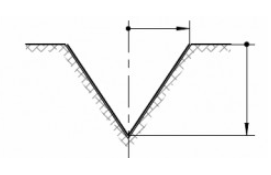
Ansatz/Problem:

Mein Ansatz A=(1/2)*g*h sowie B/2 für Hypotenuse. Pythagoras $$ \sqrt { (\frac { B }{ 2 } )^{ 2 }-(\frac { g }{ 2 } )^{ 2 } } =\quad h $$

h umgeschrieben: $$ \frac { B }{ 2 } -\frac { g }{ 2 } =h $$

$$ \frac { 1 }{ 2 } (B-g)=h $$ Nun h in Formel für A einsetzen:

$$ \frac { 1 }{ 2 } *g\frac { 1 }{ 2 } (B-g)\quad =\quad A $$

Nun A ableiten und gleich 0 setzen..

Ist dies soweit richtig oder hat sich ein Fehler eingeschlichen?

Answer 1

A = g/2 * h

Wobei (g/2)^2 + h^2 = (B/2)^2

(g/2)^2 = (B/2)^2 - h^2

Statt nun hier irgendwas mit Wurzeln zu basteln, kann man auch dafür sorgen, dass A^2 maximal wird.

A^2 = ((B/2)^2 - h^2) * h^2

Nun ausmult., ableiten und Null setzen.

Anmerkung: Wurzelziehen, um h allein zu haben, hattest du zu stark vereinfacht.

Comments

Danke Lu, war denn meine Rechnung bis jetzt soweit richtig oder einfach falsch ?

Ich komme immer auf h =(B/2)-(g/2)  ich habe die Wurzel durch ein Potenzgesetz ersetzt

---

A²(h) = ((B/2)² - h²) * h^2       

= (B/2)^2 * h^2 - h^4

(A^2(h))' = 2h(B/2)^2 - 4h^3 = 0     |:h, da h sicher grösser 0, kann die Lösung h=0 vernachlässigt werden.

4h^2 = 2(B/2)^2

h^2 = (B/2)^2 / 2 = B^2/8

h = B / (2√2)

g/2 = √((B/2)^2 - h^2) 

= √(B^2/4 - B^2/ (4*2)) = B√((2-1)/8)= B/√8 = B/√8

g/2 = B/√8 = B/(√2)

(Rechnung ohne Gewähr! Sorgfältig nachrechnen.)

---

"Ich komme immer auf h =(B/2)-(g/2)  ich habe die Wurzel durch ein Potenzgesetz ersetzt "

Genau das ist falsch.

4^2 + 3^2 = 5^2

aber 4 + 3 ≠ 5

---

Ah okay. Macht Sinn. Aber warum setzt du das ganze für g ein und nicht für h. Für h ist es doch einfacher oder nicht

---

Probier es umgekehrt und vergleiche dann die Resultate zur Kontrolle.

---

Nochmal kurz nachgefragt, dann  hab ich alles.

A²(h) = ((B/2)² - h²) * h 

müsste wenn man A^2 hat dort nicht: ((B/2)² - h²) * h^2 // auch h mit h^2 heißen ? 

---

Guter Einwand. Danke. Rechne das besser so, wie du das vorschlägst.

EDIT: Habe oben etwas rumkorrigiert. (Weiterhin ohne Gewähr)

---

Einmal muss ich noch etwas einwerfen g = B*√3/ 8

das muss doch eigentlich: \( g=\frac{3 B^{2}}{8} \) heißen.

Ich habe meinen Verdacht mal überprüfen lassen. Gleichung zu der gelöst werden soll ist x.

Lu ich weiß, dass du echt was auf dem Kasten hast, aber kann das sein, dass du ein ^2 vergessen hast ?

---

mit g = 3B^2/8 hättest du einen Dimensionskonflikt.

g berechnet man mit Pyhtagoras. Da ist schon ein Wurzel nötig.

Kontrolle mit https://www.wolframalpha.com/input/?i=f%28x%29+%3D+%28%28B%2F2%29%5E2+-+x%5E2%29+*+x%5E2

hat mich aber noch auf einen Ableitungsfehler zu Beginn gebracht.

Rechung wurde inzwischen editiert (blau).

---

Ich muss noch etwas einwerfen:

g/2 = √((B/2)² - h²)  

wir setzen h ein, das ist klar. Aber wir setzen dies doch in diese Gleichung ein:

(g/2)² = (B/2)² - h² 

wurde ganz oben ein ^2 vergessen ? (g/2 = √((B/2)² - h²) ) zu (g/2)² = (B/2)² - h² 

Also g = B/sqrt(2)

---

Lu das was du meinst mit g/2 = √((B/2)² - h²)  

\( \frac{g}{2}=\sqrt{\left(\frac{B}{2}\right)^{2}-\left(\frac{B}{\sqrt{8}}\right)^{2}} \)
\( g=\frac{\sqrt{B^{2}}}{\sqrt{2}} \)

Das was ich meine:

\( \left(\frac{g}{2}\right)^{2}=\left(\frac{B}{2}\right)^{2}-\left(\frac{B}{\sqrt{8}}\right)^{2} \)
\( g=\frac{B}{\sqrt{2}} \)

---

Gast: Da besteht kein Unterschied, da B als Breite einer Kunststoffplane eine positive Zahl sein muss.

---

(B/2)^2 - (B/√8)^2 = B^2/4 - B^2/8

= 2B^2/8 - B^2/8 = B^2/8

Also

(g/2)^2 = B^2/8

g^2/4 = B^2/8

g^2 = B^2/2

g = B/√2