Monotonie. Monotoniebereiche für f(x) = -x^3 + 6x^2 angeben.

Question

Ich habe hier die Gleichung f(x) = -x³+6x² und soll für diese die Monotoniebereiche angeben und das Verhalten von x→±∞.

Ich weiß nicht, wie ich dabei vorgehen muss und hoffe, dass es mir jemand relativ simpel gehalten erklären kann.

LG :-)

Answer 1

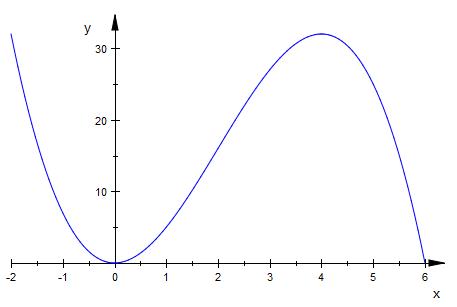
f ( x ) = -x³ + 6 * x²

f ´( x ) = -3*x^2 + 12 * x

Extremwerte
-3*x^2 + 12 * x = 0
x * ( -3 * x + 12 ) = 0
Ein Produkt ist dann 0 wenn mindestens einer der Faktoren 0 ist
x = 0
und
-3 * x + 12 = 0
x = 4

Monotonie > 0
-3*x^2 + 12 * x > 0
x * ( -3 * x + 12 ) > 0

1.Fall ( plus mal plus )
( x > 0  ) und  ( -3 * x + 12 ) > 0
-3 * x + 12  > 0
12 > 3 * x
x < 4
Zusammen ( x > 0 ) und ( x < 4 ) => 0 < x < 4
Für  0 < x < 4 ist die Funktion steigend

2.Fall ( minus mal minus )
( x < 0  ) und  ( -3 * x + 12 ) < 0
-3 * x + 12  < 0
12 < 3 * x
x > 4
Zusammen ( x < 0 ) und ( x > 4 ) : keine Schnittmenge

steigend : 0 < x < 4
fallend : x < 0  und x > 4

Answer 2

$$f'(x)=-3x^2+12x$$

Für welche Werte von x gilt f'(x)=0?