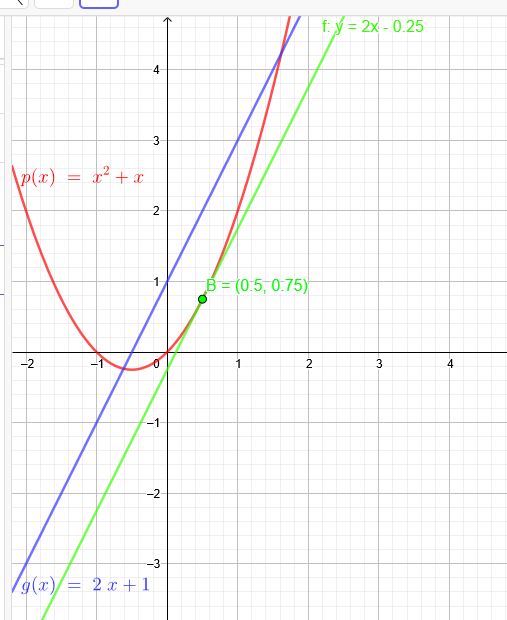
Ohne Ableitung:
\(p(x)=x^2+x\) \(g(x)=2x+1\) → \(y=2x+n\) geschnitten mit \(p(x)=x^2+x\):
\(x^2+x=2x+n\)
\(x^2-x=n\) quadratische Ergänzung:
\(x^2-1x+0,5^2=n+0,5^2\) 2.Binom:
A) \((x-\red{0,5})^2=n+0,25 |± \sqrt{~~} \)
\(x-0,5=± \sqrt{n+0,25} \) Im Fall \(n+0,25=0 \) liegt Berührung vor.
\(n=- 0,25 \) Tangente \(y=2x- 0,25\)
Berührpunkt B\((\red{0,5}| 0,75 )\)
Man sieht an Zeile A) auch, dass die Berührpunktstelle bei \(x=\red{0,5}\) ohne weitere Berechnung liegt.