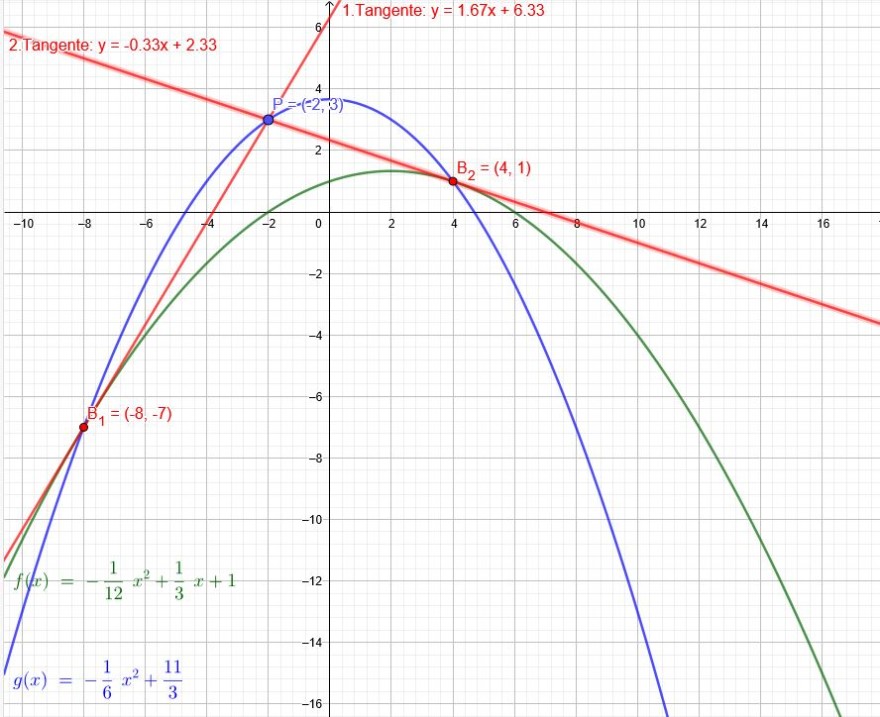
Vom Punkt \(P( -2 | 3 )\) aus werden die Tangenten an die Funktion \(f(x)= -\frac{1}{12} x^2 + \frac{1}{3}x + 1\) gelegt.
Wie lauten die Gleichungen der Tangenten?
\(f´(x)= -\frac{1}{6} x + \frac{1}{3}\)
\( \frac{y-3}{x+2}=-\frac{1}{6} x + \frac{1}{3} \)
\( y=-\frac{1}{6} x^2+\frac{11}{3}\)
\( -\frac{1}{12} x^2 + \frac{1}{3}x + 1=-\frac{1}{6} x^2+\frac{11}{3}\)
\( - x^2 + 4x + 12=-2 x^2+44\)
\( x^2 + 4x =32\)
\( (x + 2)^2 =32+4=36\)
1.)
\( x + 2=6\)
\( x_1=4\) \(f(4)= -\frac{1}{12} \cdot 16 + \frac{1}{3}\cdot 4 + 1=1\)
2.)
\( x + 2=-6\)
\( x_2 =-8\) \(f(-8)= -\frac{1}{12}\cdot 64 + \frac{1}{3}\cdot(-8) + 1=-7\)
\(B_1(4|1)\) und \(B_2(-8|-7)\)
\(f´(4)= -\frac{1}{6} \cdot4 + \frac{1}{3}=-\frac{1}{3}\)
\(f´(-8)= -\frac{1}{6} \cdot(-8) + \frac{1}{3}=\frac{5}{3}\)
Nun lassen sich mit der Punkt-Steigungsform der Geraden:\( \frac{y-y_B}{x-x_B}=m \) die Tangenten berechnen.