Durch den Punkt P (2/11) sind Tangenten an den Kreis k zu legen, der den Mittelpunkt M (0/-3) und den Radius r= 10 hat.

Question

Ich habe ein Problem mit diesem Beispiel:

Durch den Punkt P (2/11) sind Tangenten an den Kreis k zu legen, der den Mittelpunkt M (0/-3) und den Radius r= 10 hat. Geben sie Gleichungen der Tangenten an!

Ich weiß leider gar nicht, wie das gehen soll :(

Bitte helft mir :)

Comments

vielen Dank!
Kann man dies nicht auch noch anders berechnen? ich habe hier in meinen Unterlagen noch stehen:

Wir erstellen eine Hilfsgerade "Polare" durch Spaltform: ( x-3) * (x-3) + (y+6) * ( y+6)=20 und setzen die Koordinaten des Pol`s für x ein und ein y in die Spaltform ein

---

Wenn das in deinen Unterlagen steht, solltest du eigentlich mit folgender Wikipediaseite etwas anfangen können:

https://de.wikipedia.org/wiki/Pol_und_Polare

Answer 1

Alle Geraden die durch den Punkt (2, 11) gehen haben die Funktionsgleichung

y = a·(x - 2) + 11 = a·x - 2·a + 11
a·x - y - 2·a + 11 = 0

Diese sollen zugleich den Abstand 10 vom Punkt M (0, -3) haben

d = |a·(0) - (-3) - 2·a + 11| / √(a^2 + 1) = 10
|- 2·a + 14| / √(a^2 + 1) = 10
|2·a - 14| = 10√(a^2 + 1)
4·a^2 - 56·a + 196 = 100·(a^2 + 1)
96·a^2 + 56·a - 96 = 0
12·a^2 + 7·a - 12 = 0
a = 3/4 ∨ a = - 4/3

Damit lauten die Tangenten

y = 3/4·(x - 2) + 11
y = -4/3·(x - 2) + 11

Skizze:

Answer 2

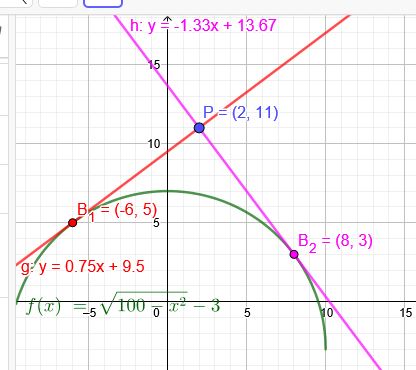
Durch den Punkt \(P (2|11)\) sind Tangenten an den Kreis k zu legen, der den Mittelpunkt \(M (0|-3)\) und den Radius \(r= 10\) hat. Geben sie Gleichungen der Tangenten an!

 \(x^2+(y+3)^2=100\) →    \((y+3)^2=100-x^2\)

Ich beachte jetzt nur den + Teil→  \(y=\sqrt{100-x^2}-3\)  →  \(y´=-\frac{x}{\sqrt{100-x^2}}\)

Berührpunkte sind

\(B(x|\sqrt{100-x^2}-3)\)

\( \frac{\sqrt{100-x^2}-3-11}{x-2}=-\frac{x}{\sqrt{100-x^2}} \)

\( \frac{\sqrt{100-x^2}-14}{x-2}=-\frac{x}{\sqrt{100-x^2}} \)

\( \frac{\sqrt{100-x^2}-14}{2-x}=\frac{x}{\sqrt{100-x^2}} \)

\(100-x^2-14 \cdot \sqrt{100-x^2}=2x-x^2  \)

\(14 \cdot \sqrt{100-x^2}=100-2x \)

\(14^2 \cdot (100-x^2)=(100-2x)^2 \)

\(x_1=-6\)   \(y(-6)=5\)     \(y´(-6)=\frac{3}{4}\)

\(x_2=8\)  \(y=3\)    \(y´=-\frac{4}{3}\)

Jetzt die Tangenten aufstellen.