Winkel in räumlichem Dreiecksgebilde

Question

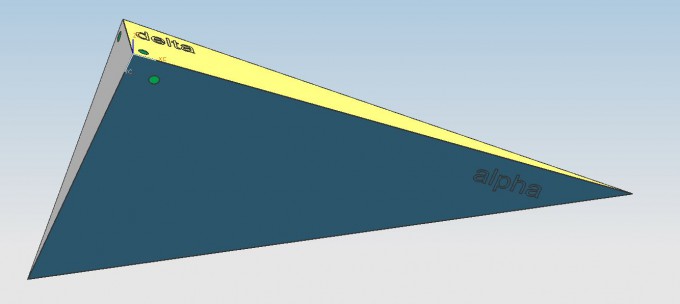
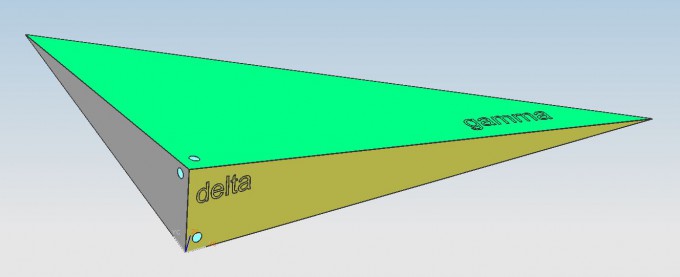
Ein räumliches Gebilde ist aus 4 rechtwinkligen Dreiecken zusammengesetzt.

Alle Kanten liegen exakt aufeinander und umschließen einen Raum.

Von zwei Dreiecken ist ein Winkel bekannt, Alpha und Gamma.

Gesucht ist der Winkel Delta.

Ich komme auf 7 Gleichungen mit 7 Unbekannten, krieg die aber nicht aufgelöst....

Die rechten Winkel sind auf den Bildern mit einem Loch markiert.

Comments

Wo ist Alpha? EDIT: Alpha ist nun zu sehen.

7 Gleichungen mit 7 Unbekannten sollten an sich genügen.

Wenn keine Seite gegeben ist, kannst du einfach eine festlegen und dann die übrigen schrittweise ausrechnen, bis du alle zwei Seiten des gelb-grünen Dreiecks kennst.

Die fraglichen Körper wären ja alle ähnlich zueinander.

---

Alpha ist im oberen Bild, im blauen Dreieck. Da wo Alpha steht.

---

Wenn keine Seite gegeben ist, kannst du einfach eine festlegen und dann die übrigen schrittweise ausrechnen, bis du alle zwei Seiten des gelb-grünen Dreiecks kennst.

Die fraglichen Körper wären ja alle ähnlich zueinander.

---

Das nutzt mir nichts, ich brauch die Formel Delta(Alpha, Gamma).

---

Die festgelegte Seite wird sich irgendwann wegkürzen lassen.

Answer 1

du scheinst es dir sehr umständlich zu machen. Folgende Beziehungen liegen vor

$$ \cos(\alpha) = \frac{a}{c}, \quad \cos(\gamma) = \frac{a'}{c} \quad \sin(\delta) = \frac{a}{a'} $$

Somit also

$$ \sin(\delta) = \frac{\cos(\alpha)}{\cos(\gamma)} $$

Welche Seiten ich mit \(a, a', c\) meine kannst du dir ja ganz schnell selbst überlegen.

Gruß

Comments

Suuuper, vielen Dank.

Manfred