Textaufgabe: Offene Kegel formen - Volumen berechnen und vergleichen

Question

Aus einem Viertelkreis, einem Halbkreis und einem Dreiviertelkreis, jeweils mit dem Radius 10 cm, werden offene Kegel geformt. Berechne und vergleiche ihr Volumen. Beachte dabei den Unterschied zwischen dem Radius der Mantelfläche und dem Grundkreisradius.

Kann mir jemand zeigen wie man das rechnet? Danke.

Answer 1

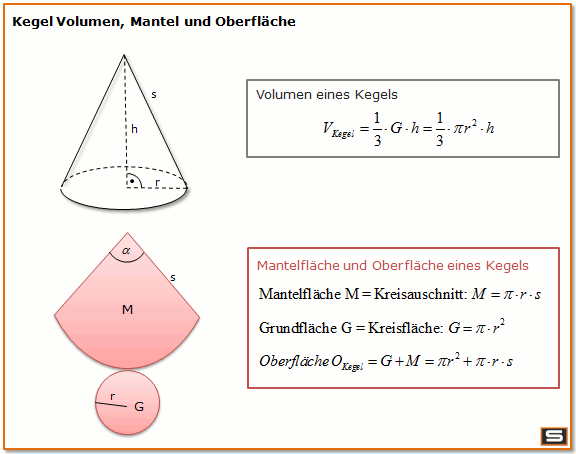
- Ich mach dir den Viertelkreis einmal vor
- Viertelkreis hat einen Winkel α von 90° 
- Der Radius sowie die Seitenlänge sind 10 cm 
- 1.) Wir wollen nun aber, für das Volumen den Radius des entstehenden Kreises berechnen.
- Dafür schauen wir uns erst einmal den Umfang des Kegelkreises an
- Daher ist Umfang_Kreis =( π * r_Viertelkreis * α) / 180 . .
- Nun setzen wir die Werte ein :  Umfang =( π * 10cm * 90°) / 180 =15,71 cm.
2.) Jetzt rechnen wir das ganze rückwärts. . 15,71= 2 π r . . 15,71:2π= r = 2,498cm. 
- Nun der Satz des Pythagoras: h= √ 10² - 2,498²   = 9.68cm
- Jetzt haben wir alles für das Volumen:   1/3* πr² *h = 63,37 cm³

So fährst du auch bei den anderen fort, musst dies dann eben ins Verhältnis setzen.