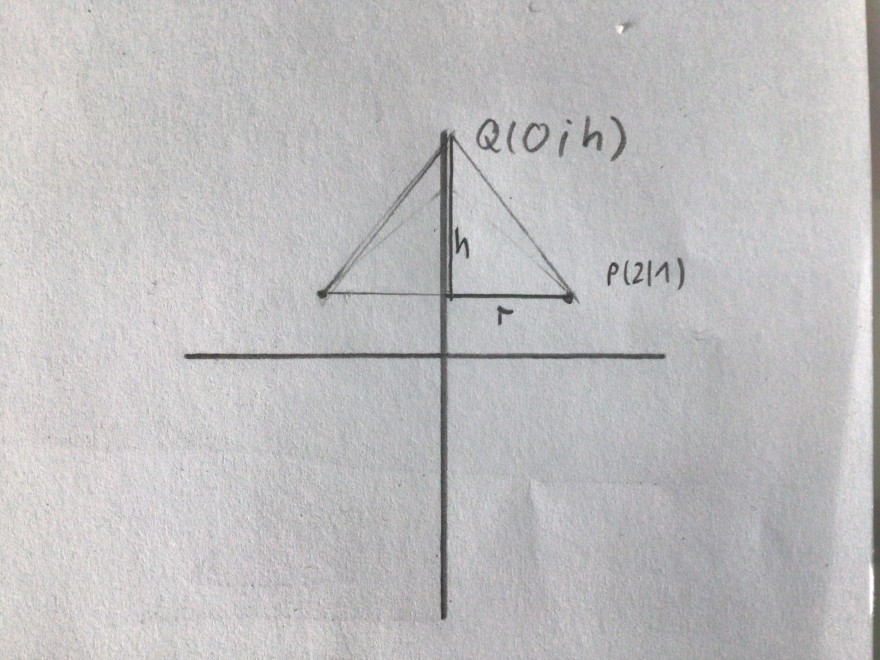
Aufgabe:
Die Gerade g verläuft durch die Punkte P(2;1) und Q(0;h) mit h>1. Sie bildet mit den Koordinatenachsen ein Dreieck. Dieses Dreieck rotiert um die y-Achse. Dabei entsteht ein Kegel. Für welchen Wert von h hat das Volumen dieses Kegels einen extremalen Wert? Welcher Art ist dieses Extremum? (Es war keine Skizze vorgegeben. Die sich unten befindliche Skizze, ist, meiner Meinung nach, so gemeint, wie es die Aufgabenstellung meint.)
Problem/Ansatz:
Meine Vermutung ist, dass es sich um ein Minimum handelt, da mit zunehmender Höhe, das Volumen immer größer werden würde. Wir wissen, dass der Radius r=2 ist und h größer als 1 sein muss. Die Formel für das Volumen ist auch klar, also V=1/3 πr^2 h.
Nun liegt das Problem in der Zielfunktion. Wenn ich r=2 in die Volumenformel einsetzen würde, entsteht eine lineare Funktion ohne Extrempunkte. Wenn ich aber mithilfe der Formel s^2=r^2+h^2 versuche r zu ersetzen, um h zu erhalten, um auf eine Funktion mit Extrempunkten zu kommen, dann habe ich eine weitere Unbekannte, nämlich s, die nicht gegeben ist. Dann habe ich versucht s zu ersetzen, indem ich letztere Formel umgestellt und das jeweils dafür eingesetzt habe. Doch letztendlich macht meine Zielfunktion noch immer keinen Sinn und übereinstimmend ist die auch nicht.
Nun brauche ich, hinsichtlich der Zielfunktion, Hilfe, denn ich komme zu keiner sinnvollen Funktion und habe nun schon alles ausprobiert, was mir eingefallen ist.