Funktion anhand des Graphen erraten

Question

hat jemand eine Idee, wie ich bei diesem Graphen die Funktion erraten kann?
Ich habe an Daten bis jetzt nur:
f(x)= ax^3+bx^2+cx+d

bx^2 würde ich rauswerfen, weil der Graph nicht symmetrisch ist
P(0|0) d=0
f'(-2)=0
f'(1)=0

Ich bin mir bei der Aufgabe nicht sicher, ob ich die raten kann oder ob man die suchen muss. In der Aufgabe gibt es keine weiteren Beschriftungen. Die Extrema sind aber eindeutig würde ich sagen und können verwendet werden.

Answer 1

f(x)= ax³+bx²+cx+d      gut

bx² würde ich rauswerfen, weil der Graph nicht symmetrisch ist 

Darfst du nicht einfach rauswerfen. Ein x^2 allein macht noch keine Symmetrie.
P(0|0) d=0     richtig!
f'(-2)=0     richtig!
f'(1)=0         richtig! 

Nimm vielleicht noch f(1.75) = 0. Ist aber vielleicht nicht ganz genau. 

Answer 2

Wichtig ist erstmal zu schauen, ob der Graph Symmetrisch zum Ursprung, oder zur y-Achse ist.

Danach schaut man, wie viele Nullstellen möglich wären, in diesem Fall 3, bedeutet: Dein höchster Exponent muss 3 sein, sprich x³.

Des weiteren kannst du eine Art Ordinatenaddition durchführen, heißt, in was für funktionen könnte man diese funktion zerlegen.

Als wichtigster Punkt natürlich der Schnittpunkt mit der y-Achse, um das Absolutglied zu bestimmen.

In diesem Fall wäre die Funktion ungefähr wie folgt lauten:

f(x)=ax³+bx²-cx

Begründung, -cx, da man eine negative gerade ziehen kann, welche durch den Wendepunkt geht (Ungefähr -2x oder -3x), Das Absolutglied ist Null, da der Graph durch den Ursprung geht.

das bx² darfst du wie bereits erwähnt nicht einfach rauswerfen, da der Graph auf der x-Achse verschoben wurde ;)

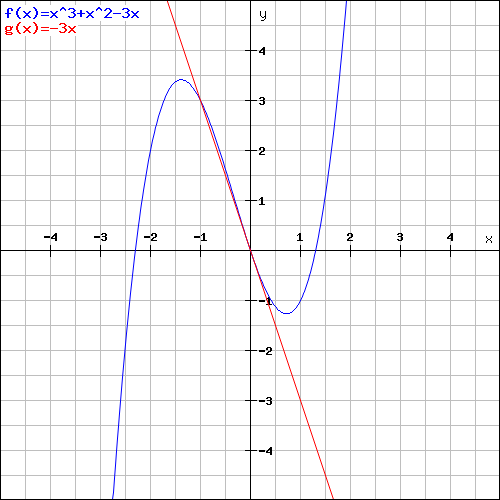
Rot ist y=-3x, kommt ungefähr hin, wenn die funktion lautet f(x)=x³+x²-3x

Die Faktoren vor dem x³ und dem x² können sich natürlich noch ändern, man benötigt halt die genauen Nullstellen etc.

Answer 3

wenn man \(f(-3)=\dfrac32\) als zusätzliche Information annimmt, kommt man auf \(f(x)=\dfrac13x^3+\dfrac12x^2-2x\). Dazu passen auch die Nullstellen relativ gut.