Hallo Asura,
Wollkommen in der Mathelounge!
Muss ich einfach wild jede Möglichkeit durchgehen und hoffen, dass eine funktioniert?
Nein, das muss man nicht. Ich gehe davon aus, dass eine Tiefen- bzw. Breitensuche vollständig ist. D.h. ausgehend von Startknoten werden alle Knoten eines zusammen hängen Graphen besucht.
Bei der Suche \(T_1\) gehen vom Startknoten drei Kanten ab. Im Graphen oben gibt es nur 2 Knoten mit drei Kanten. Das sind die Knoten 4 und 10. Anschließend gibt es zwei 'Sackgassen'. D.h. Pfade, die zu einem Knoten mit eben nur dieser einen Kante führen oder zu einem Knoten, von dem kein Knoten erreichbar ist, der nicht schon im Suchpfad liegt.
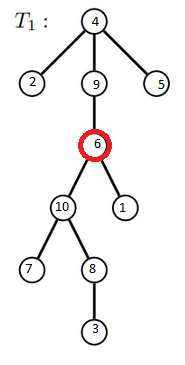
Wenn man bei \(s=4\) beginnt, müsste der Knoten 6 der rot markierte sein und der Weg zu 1 ist eine 'Sackgasse'. Und dies würde passen. \(T_1\) ist ein möglicher Suchbaum!
Bei \(T_2\) hat der Startknoten 2 Kanten. Damit kommen die Knoten 2, 3, 8 und 9 in Frage. Die Knoten 2 und 9 scheiden aus, da keiner der beiden Nachbarknoten 4 und 6 in einer Sackgasse liegen kann. Startet man beim Knoten 3, so kann nur 8 die Sackgasse sein. Dann gehen aber von 6 zwei Sackgassen ab, und das wiedrum ist nicht möglich!
Bleibt als Startknoten der Knoten 8. Das ist auch keine Lösung, da keiner der Nachbarknoten 3 und 10 über 4 weitere Kanten verfügt. \(T_2\) kann daher kein Suchbaum sein.
Gruß Werner