Beziehung besteht zwischen den Steigungen zweier aufeinander normal stehender Geraden?

Question

fragen zu funktionen bitte lösen :)

1. Welche Beziehung besteht zwischen den Steigungen zweier aufeinander normal stehender Geraden?

2. Wie müsste demnach die Gleichung der x-Achse lauten?

3. Wie müsste demnach die Gleichung der y-Achse lauten?

Answer 1

1. Welche Beziehung besteht zwischen den Steigungen zweier aufeinander normal stehender Geraden?

Das Produkt der Steigungen ist -1

2. Wie müsste demnach die Gleichung der x-Achse lauten?

y = 0*x

3. Wie müsste demnach die Gleichung der y-Achse lauten?

y = 1/0*x
1/0 ist allerdings nicht erlaubt da wir nicht durch 0 teilen dürfen.
Die Gleichung der y-Achse lautet x = 0. Es ist KEINE Funktionsgleichung.

Answer 2

1. Welche Beziehung besteht zwischen den Steigungen zweier aufeinander
normal stehender Geraden?

m1 = - 1 / m2

2. Wie müsste demnach die Gleichung der x-Achse lauten?

y = 0 * x

3. Wie müsste demnach die Gleichung der y-Achse lauten?

m1 = - 1 / 0
Ist nicht definiert. Division durch 0.

Ansonsten : Für alle Punkte der y-Achse gilt x = 0

Answer 3

man kann sich eine kleine Skizze machen und daraus schnell ersehen, dass die Steigung der zweiten Geraden, wenn man die Steigung der ersten Geraden als m bezeichnet, -1/m beträgt:

 

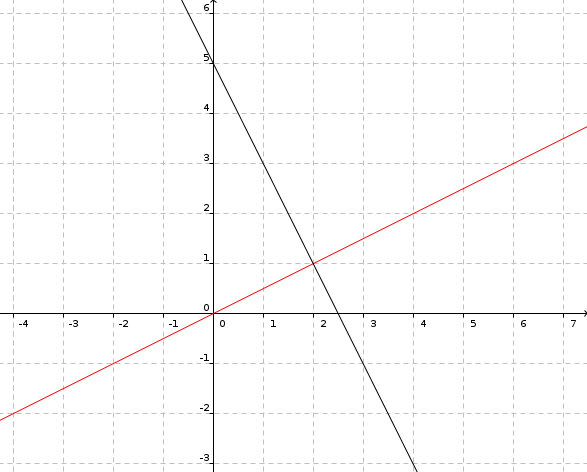
Hier hat die rote Gerade die Steigung 1/2, die schwarze hat dann die Steigung -2/1 = -2.

Geradengleichung allgemein: y = mx + b

Gleichung der x-Achse also

f(x) = 0 * x + 0 = 0

Die Gleichung der y-Achse ist nicht so einfach aufzustellen, da man ja nicht durch 0 dividieren darf. 

Ich würde einfach schreiben: 

x = 0

(bin mir aber hier nicht sicher, ob das mathematisch "sauber" ist.)

Besten Gruß